Next: Diffraction from Rectangular Slit Up: Wave Optics Previous: Diffraction from Rectangular Aperture Contents
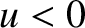 , which implies that the
edge corresponds to
, which implies that the
edge corresponds to 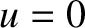 . In other words, suppose that
. In other words, suppose that 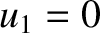 and
and
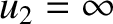 . It is easily demonstrated that
. It is easily demonstrated that
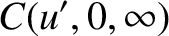 |
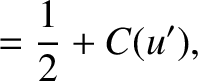 |
(10.128) |
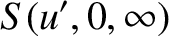 |
 |
(10.129) |
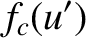 |
![$\displaystyle = \frac{1}{2}\left[ C(u')-S(u')\right],$](img3645.png) |
(10.130) |
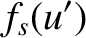 |
![$\displaystyle =\frac{1}{2}\left[ 1+ C(u')+S(u')\right],$](img3646.png) |
(10.131) |
The intensity of the diffraction pattern of a semi-infinite opaque plane is shown in Figure 10.17.
Note that this is an intrinsically near-field diffraction pattern [because the aperture is of infinite extent; see Equation (10.96)].
In the directly illuminated region, 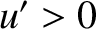 , the
intensity oscillates with diminishing amplitude, as the distance from the edge increases, and
asymptotically approaches the value
, the
intensity oscillates with diminishing amplitude, as the distance from the edge increases, and
asymptotically approaches the value
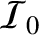 , as would be expected on the basis of
geometric optics. In the shadow region,
, as would be expected on the basis of
geometric optics. In the shadow region, 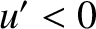 , the intensity
decreases monotonically towards zero as the distance from the edge increases.
Note that the maximum value of
the intensity is not at the edge of the geometric shadow (i.e.,
, the intensity
decreases monotonically towards zero as the distance from the edge increases.
Note that the maximum value of
the intensity is not at the edge of the geometric shadow (i.e.,  ), but some
distance away from it, in the directly illuminated region. Finally, at the
edge of the shadow,
), but some
distance away from it, in the directly illuminated region. Finally, at the
edge of the shadow,
 . This is to be expected because half the wavefront is obstructed, the amplitude of the wave at the projection screen is thus halved, and the intensity consequently drops to one quarter of the unobstructed intensity.
. This is to be expected because half the wavefront is obstructed, the amplitude of the wave at the projection screen is thus halved, and the intensity consequently drops to one quarter of the unobstructed intensity.