Next: Diffraction from Straight Edge Up: Wave Optics Previous: Babinet's Principle Contents
![\begin{displaymath}f(u,v) = \left\{
\begin{array}{lll}
1&\mbox{\hspace{0.5cm}}& ...
... ~$v_1<v<v_2$}\\ [0.5ex]
0&&\mbox{otherwise}\end{array}\right.,\end{displaymath}](img3612.png) |
(10.118) |
 and
and 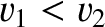 .
In this case, the two-dimensional integrals in Equations (10.103) and (10.104) are separable.
Using some standard trigonometric identities (see Section B.3), we obtain
where
Here, the functions
.
In this case, the two-dimensional integrals in Equations (10.103) and (10.104) are separable.
Using some standard trigonometric identities (see Section B.3), we obtain
where
Here, the functions
 |
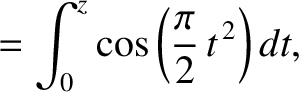 |
(10.123) |
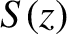 |
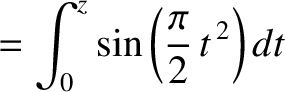 |
(10.124) |
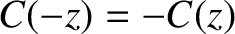 ,
,
 , and
, and
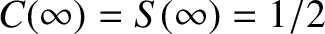 . The Frensel integrals are plotted in Figure 10.16.
. The Frensel integrals are plotted in Figure 10.16.
Suppose that the aperture is of infinite extent in the  -direction, which implies that
-direction, which implies that
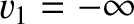 and
and
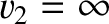 . In this case, the aperture becomes a rectangular slit running parallel to the
. In this case, the aperture becomes a rectangular slit running parallel to the  -axis, and
extending from
-axis, and
extending from 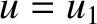 to
to 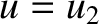 .
It is easily seen that
.
It is easily seen that
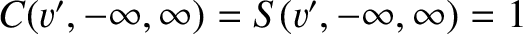 . Hence, Equations (10.119) and
(10.120) yield
. Hence, Equations (10.119) and
(10.120) yield