


Next: Worked example 6.6: 2-dimensional
Up: Conservation of momentum
Previous: Worked example 6.4: Bullet
Question: An object of mass
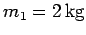 , moving
with velocity
, moving
with velocity
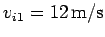 , collides head-on with
a stationary object whose mass is
, collides head-on with
a stationary object whose mass is
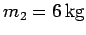 . Given that the collision
is elastic, what are the final velocities of the two objects. Neglect friction.
. Given that the collision
is elastic, what are the final velocities of the two objects. Neglect friction.
Answer: Momentum conservation yields
where 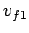 and
and 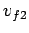 are the final velocities of the first and second
objects, respectively. Since the collision is elastic, the total kinetic
energy must be the same before and after the collision. Hence,
are the final velocities of the first and second
objects, respectively. Since the collision is elastic, the total kinetic
energy must be the same before and after the collision. Hence,
Let
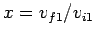 and
and
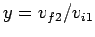 . Noting that
. Noting that 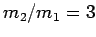 , the above two
equations reduce to
, the above two
equations reduce to
and
Eliminating  between the previous two expressions, we obtain
between the previous two expressions, we obtain
or
which has the non-trivial solution 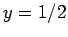 . The corresponding solution for
. The corresponding solution for  is
is
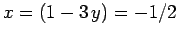 .
.
It follows that the final velocity of the first object is
The minus sign indicates that this object reverses direction as a
result of the collision. Likewise, the final velocity of the second object is



Next: Worked example 6.6: 2-dimensional
Up: Conservation of momentum
Previous: Worked example 6.4: Bullet
Richard Fitzpatrick
2006-02-02
![]() and
and
![]() . Noting that
. Noting that ![]() , the above two
equations reduce to
, the above two
equations reduce to