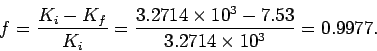Next: Worked example 6.5: Elastic
Up: Conservation of momentum
Previous: Worked example 6.3: Skater
Question: A bullet of mass 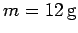 strikes a stationary wooden block
of mass
strikes a stationary wooden block
of mass
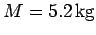 standing on a frictionless surface. The block, with
the bullet embedded in it, acquires a velocity of
standing on a frictionless surface. The block, with
the bullet embedded in it, acquires a velocity of
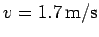 . What
was the velocity of the bullet before it struck the block? What fraction of the
bullet's initial kinetic energy is lost (i.e., dissipated) due to
the collision with the block?
. What
was the velocity of the bullet before it struck the block? What fraction of the
bullet's initial kinetic energy is lost (i.e., dissipated) due to
the collision with the block?
Answer: Let  be the initial velocity of the bullet.
Momentum conservation requires the total horizontal momentum of the
system to be the same before and after the bullet strikes the block.
The initial momentum of the system is simply
be the initial velocity of the bullet.
Momentum conservation requires the total horizontal momentum of the
system to be the same before and after the bullet strikes the block.
The initial momentum of the system is simply  , since the
block is initially at rest. The final momentum is
, since the
block is initially at rest. The final momentum is 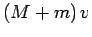 , since
both the block and the bullet end up moving with velocity
, since
both the block and the bullet end up moving with velocity  . Hence,
. Hence,
giving
The initial kinetic energy of the bullet is
The final kinetic energy of the system is
Hence, the fraction of the initial kinetic energy which is dissipated is



Next: Worked example 6.5: Elastic
Up: Conservation of momentum
Previous: Worked example 6.3: Skater
Richard Fitzpatrick
2006-02-02
![]() be the initial velocity of the bullet.
Momentum conservation requires the total horizontal momentum of the
system to be the same before and after the bullet strikes the block.
The initial momentum of the system is simply
be the initial velocity of the bullet.
Momentum conservation requires the total horizontal momentum of the
system to be the same before and after the bullet strikes the block.
The initial momentum of the system is simply ![]() , since the
block is initially at rest. The final momentum is
, since the
block is initially at rest. The final momentum is ![]() , since
both the block and the bullet end up moving with velocity
, since
both the block and the bullet end up moving with velocity ![]() . Hence,
. Hence,