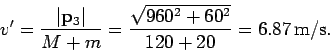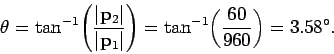Next: Worked example 6.4: Bullet
Up: Conservation of momentum
Previous: Worked example 6.2: Hitting
Question: A skater of mass
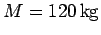 is skating across a pond
with uniform velocity
is skating across a pond
with uniform velocity
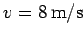 . One of the skater's friends, who is
standing at the edge of the pond, throws a
medicine ball of mass
. One of the skater's friends, who is
standing at the edge of the pond, throws a
medicine ball of mass
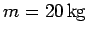 with velocity
with velocity
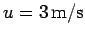 to the skater, who catches
it. The direction of motion of the ball is perpendicular to the initial direction of motion
of the skater.
What is the final speed of the skater? What is the final direction
of motion of the skater relative to his/her initial direction of motion? Assume that the
skater moves without friction.
to the skater, who catches
it. The direction of motion of the ball is perpendicular to the initial direction of motion
of the skater.
What is the final speed of the skater? What is the final direction
of motion of the skater relative to his/her initial direction of motion? Assume that the
skater moves without friction.
Answer: Suppose that the skater is initially moving along the  -axis, whereas
the initial direction of motion of the medicine ball is along the
-axis, whereas
the initial direction of motion of the medicine ball is along the 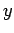 -axis. The skater's
initial momentum is
-axis. The skater's
initial momentum is
Likewise, the initial momentum of the medicine ball is
After the skater catches the ball, the combined momentum of the skater
and the ball is
This follows from momentum conservation. The final speed of the skater (and the ball)
is
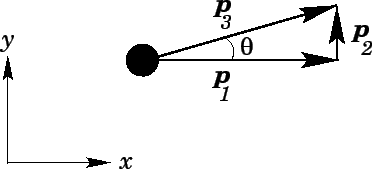
The final direction of motion of the skater is parameterized by the angle 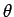 (see the above diagram), where
(see the above diagram), where



Next: Worked example 6.4: Bullet
Up: Conservation of momentum
Previous: Worked example 6.2: Hitting
Richard Fitzpatrick
2006-02-02

![]() -axis, whereas
the initial direction of motion of the medicine ball is along the
-axis, whereas
the initial direction of motion of the medicine ball is along the ![]() -axis. The skater's
initial momentum is
-axis. The skater's
initial momentum is