


Next: Worked example 6.3: Skater
Up: Conservation of momentum
Previous: Worked example 6.1: Cannon
Question: A softball of mass
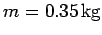 is pitched
at a speed of
is pitched
at a speed of
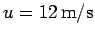 . The batter hits the ball directly back to
the pitcher at a speed of
. The batter hits the ball directly back to
the pitcher at a speed of
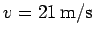 . The bat acts on the ball
for
. The bat acts on the ball
for
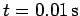 . What impulse is imparted by the bat to the ball?
What average force is exerted by the bat on the ball?
. What impulse is imparted by the bat to the ball?
What average force is exerted by the bat on the ball?
Answer: The initial momentum of the softball is 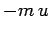 , whereas its
final momentum is
, whereas its
final momentum is 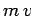 . Here, the final direction of motion of the softball
is taken to be positive. Thus, the net change in momentum of the softball due to
its collision with the bat is
. Here, the final direction of motion of the softball
is taken to be positive. Thus, the net change in momentum of the softball due to
its collision with the bat is
By definition, the net momentum change is equal to the impulse imparted
by the bat, so
The average force exerted by the bat on the ball is simply the net impulse divided by the
time interval over which the ball is in contact with the bat. Hence,



Next: Worked example 6.3: Skater
Up: Conservation of momentum
Previous: Worked example 6.1: Cannon
Richard Fitzpatrick
2006-02-02
![]() , whereas its
final momentum is
, whereas its
final momentum is ![]() . Here, the final direction of motion of the softball
is taken to be positive. Thus, the net change in momentum of the softball due to
its collision with the bat is
. Here, the final direction of motion of the softball
is taken to be positive. Thus, the net change in momentum of the softball due to
its collision with the bat is