


Next: Worked example 6.2: Hitting
Up: Conservation of momentum
Previous: Collisions in 2-dimensions
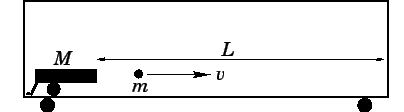
Question: A cannon is bolted to the floor of a railway carriage, which is
free to move without friction along a straight track. The combined mass of the cannon and
the carriage is
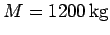 . The cannon fires a cannonball, of mass
. The cannon fires a cannonball, of mass
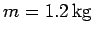 ,
horizontally with velocity
,
horizontally with velocity
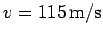 . The cannonball travels the length of the
carriage, a distance
. The cannonball travels the length of the
carriage, a distance 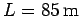 , and then becomes embedded in the carriage's end wall. What is the recoil
speed of the carriage right after the cannon is fired? What is the velocity of the
carriage after the cannonball strikes the far wall? What net distance, and in what
direction, does the carriage move as a result of the firing of the cannon?
, and then becomes embedded in the carriage's end wall. What is the recoil
speed of the carriage right after the cannon is fired? What is the velocity of the
carriage after the cannonball strikes the far wall? What net distance, and in what
direction, does the carriage move as a result of the firing of the cannon?
Answer: Conservation of momentum implies that the net horizontal momentum
of the system is the same before and after the cannon is fired. The momentum before
the cannon is fired is zero, since nothing is initially moving. Hence, we can also set the momentum after
the cannon is fired to zero, giving
where  is the recoil velocity of the carriage. It follows that
is the recoil velocity of the carriage. It follows that
The minus sign indicates that the recoil velocity of the carriage is in the
opposite direction to the direction of motion of the cannonball. Hence, the
recoil speed of the carriage is
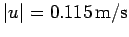 .
.
Suppose that, after the cannonball strikes the far wall of the carriage, both
the cannonball and the carriage move with common velocity 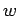 . Conservation
of momentum implies that the net horizontal momentum of the system is the same
before and after the collision. Hence, we can write
. Conservation
of momentum implies that the net horizontal momentum of the system is the same
before and after the collision. Hence, we can write
However, we have already seen that 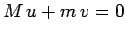 . It follows that
. It follows that  : in other
words, the carriage is brought to a complete halt when the cannonball strikes its far wall.
: in other
words, the carriage is brought to a complete halt when the cannonball strikes its far wall.
In the frame of reference of the carriage, the cannonball moves with velocity
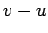 after the cannon is fired. Hence, the time of flight of the cannonball is
after the cannon is fired. Hence, the time of flight of the cannonball is
The distance moved by the carriage in this time interval is
Thus, the carriage moves
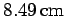 in the opposite direction to
the direction of motion of the cannonball.
in the opposite direction to
the direction of motion of the cannonball.



Next: Worked example 6.2: Hitting
Up: Conservation of momentum
Previous: Collisions in 2-dimensions
Richard Fitzpatrick
2006-02-02

![]() . Conservation
of momentum implies that the net horizontal momentum of the system is the same
before and after the collision. Hence, we can write
. Conservation
of momentum implies that the net horizontal momentum of the system is the same
before and after the collision. Hence, we can write
![]() after the cannon is fired. Hence, the time of flight of the cannonball is
after the cannon is fired. Hence, the time of flight of the cannonball is