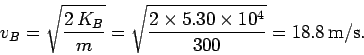Next: Worked example 5.5: Sliding
Up: Conservation of energy
Previous: Worked example 5.3: Stretching
Question: A roller coaster cart of mass
 starts
at rest at point
starts
at rest at point  , whose height off the ground is
, whose height off the ground is
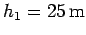 , and a
little while later reaches point
, and a
little while later reaches point  , whose height off the ground is
, whose height off the ground is
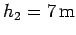 .
What is the potential energy of the cart relative to the ground at point
.
What is the potential energy of the cart relative to the ground at point  ?
What is the speed of the cart at point
?
What is the speed of the cart at point  , neglecting the effect of friction?
, neglecting the effect of friction?
Answer: The gravitational potential energy of the cart with
respect to the ground at point  is
is
Likewise, the potential energy of the cart at point  is
is
Hence, the change in the cart's potential energy in moving from point
 to point
to point  is
is
By energy conservation,
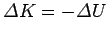 , where
, where 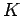 represents kinetic
energy. However, since the initial kinetic energy is zero, the change in kinetic energy
represents kinetic
energy. However, since the initial kinetic energy is zero, the change in kinetic energy
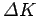 is equivalent to the final kinetic energy
is equivalent to the final kinetic energy 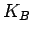 . Thus,
. Thus,
Now,
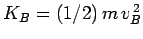 , where
, where 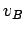 is the final speed. Hence,
is the final speed. Hence,



Next: Worked example 5.5: Sliding
Up: Conservation of energy
Previous: Worked example 5.3: Stretching
Richard Fitzpatrick
2006-02-02


![]() is
is