


Next: Worked example 5.4: Roller
Up: Conservation of energy
Previous: Worked example 5.2: Dragging
Question: The force required to slowly stretch a spring
varies from 0N to 105N as the spring is extended by 13cm
from its unstressed length. What is the force constant of the spring?
What work is done in stretching the spring? Assume that the spring
obeys Hooke's law.
Answer:
The force 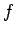 that the spring exerts on whatever is stretching it
is
that the spring exerts on whatever is stretching it
is 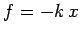 , where
, where 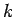 is the force constant, and
is the force constant, and  is the extension
of the spring. The minus sign indicates that the force acts in the opposite
direction to the extension. Since the spring is stretched slowly, the force
is the extension
of the spring. The minus sign indicates that the force acts in the opposite
direction to the extension. Since the spring is stretched slowly, the force
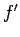 which must be exerted on it is (almost) equal and opposite to
which must be exerted on it is (almost) equal and opposite to 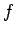 .
Hence,
.
Hence,
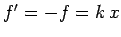 . We are told that
. We are told that 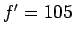 N when
N when 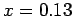 m. It
follows that
m. It
follows that
The work 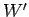 done by the external force in extending the spring from 0 to
done by the external force in extending the spring from 0 to  is
is
Hence,



Next: Worked example 5.4: Roller
Up: Conservation of energy
Previous: Worked example 5.2: Dragging
Richard Fitzpatrick
2006-02-02
![]() that the spring exerts on whatever is stretching it
is
that the spring exerts on whatever is stretching it
is ![]() , where
, where ![]() is the force constant, and
is the force constant, and ![]() is the extension
of the spring. The minus sign indicates that the force acts in the opposite
direction to the extension. Since the spring is stretched slowly, the force
is the extension
of the spring. The minus sign indicates that the force acts in the opposite
direction to the extension. Since the spring is stretched slowly, the force
![]() which must be exerted on it is (almost) equal and opposite to
which must be exerted on it is (almost) equal and opposite to ![]() .
Hence,
.
Hence,
![]() . We are told that
. We are told that ![]() N when
N when ![]() m. It
follows that
m. It
follows that