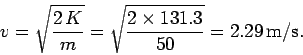Next: Worked example 5.3: Stretching
Up: Conservation of energy
Previous: Worked example 5.1: Bucket
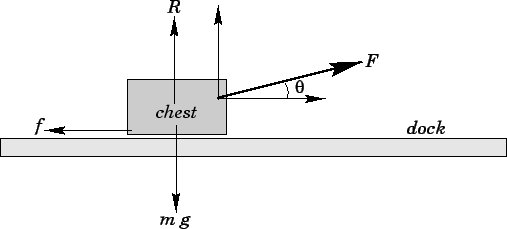
Question: A pirate drags a 50kg treasure chest over the rough
surface of a dock by exerting a constant force of 95N acting at an angle
of 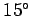 above the horizontal. The chest moves 6m in a straight line,
and the coefficient of kinetic friction between the chest and the dock is
above the horizontal. The chest moves 6m in a straight line,
and the coefficient of kinetic friction between the chest and the dock is 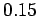 .
How much work does the pirate perform? How much energy is dissipated as heat via
friction? What is the final velocity of the chest?
.
How much work does the pirate perform? How much energy is dissipated as heat via
friction? What is the final velocity of the chest?
Answer: Referring to the diagram, the force 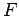 exerted by the
pirate can be resolved into a horizontal component
exerted by the
pirate can be resolved into a horizontal component 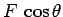 and a vertical
component
and a vertical
component 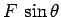 . Since the chest only moves horizontally, the vertical
component of
. Since the chest only moves horizontally, the vertical
component of 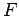 performs zero work. The work
performs zero work. The work 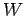 performed by the horizontal
component is simply the magnitude of this component times the horizontal distance
performed by the horizontal
component is simply the magnitude of this component times the horizontal distance
 moved by the chest:
moved by the chest:
The chest is subject to the following forces in the vertical direction:
the downward force  due to gravity, the upward reaction force
due to gravity, the upward reaction force  due to the dock, and the upward component
due to the dock, and the upward component 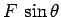 of the force
exerted by the pirate. Since the chest does not accelerate in the
vertical direction, these forces must balance. Hence,
of the force
exerted by the pirate. Since the chest does not accelerate in the
vertical direction, these forces must balance. Hence,
The frictional force 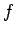 is the product of the coefficient of
kinetic friction
is the product of the coefficient of
kinetic friction 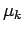 and the normal reaction
and the normal reaction  , so
, so
The work 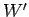 done by the frictional force is
done by the frictional force is
Note that there is a minus sign in front of the 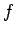 because the
displacement of the chest is in the opposite direction to
the frictional force. The fact that
because the
displacement of the chest is in the opposite direction to
the frictional force. The fact that 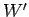 is negative indicates
a loss of energy by the chest: this energy is dissipated as
heat via friction. Hence, the dissipated energy
is
is negative indicates
a loss of energy by the chest: this energy is dissipated as
heat via friction. Hence, the dissipated energy
is
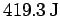 .
.
The final kinetic energy 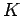 of the chest (assuming that it
is initially at rest) is the difference between the work
of the chest (assuming that it
is initially at rest) is the difference between the work 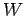 done by the pirate and the energy
done by the pirate and the energy 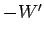 dissipated as heat.
Hence,
dissipated as heat.
Hence,
Since
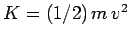 , the final velocity of the chest
is
, the final velocity of the chest
is



Next: Worked example 5.3: Stretching
Up: Conservation of energy
Previous: Worked example 5.1: Bucket
Richard Fitzpatrick
2006-02-02

![]() exerted by the
pirate can be resolved into a horizontal component
exerted by the
pirate can be resolved into a horizontal component ![]() and a vertical
component
and a vertical
component ![]() . Since the chest only moves horizontally, the vertical
component of
. Since the chest only moves horizontally, the vertical
component of ![]() performs zero work. The work
performs zero work. The work ![]() performed by the horizontal
component is simply the magnitude of this component times the horizontal distance
performed by the horizontal
component is simply the magnitude of this component times the horizontal distance
![]() moved by the chest:
moved by the chest:
![]() due to gravity, the upward reaction force
due to gravity, the upward reaction force ![]() due to the dock, and the upward component
due to the dock, and the upward component ![]() of the force
exerted by the pirate. Since the chest does not accelerate in the
vertical direction, these forces must balance. Hence,
of the force
exerted by the pirate. Since the chest does not accelerate in the
vertical direction, these forces must balance. Hence,
![]() of the chest (assuming that it
is initially at rest) is the difference between the work
of the chest (assuming that it
is initially at rest) is the difference between the work ![]() done by the pirate and the energy
done by the pirate and the energy ![]() dissipated as heat.
Hence,
dissipated as heat.
Hence,