


Next: Worked example 5.2: Dragging
Up: Conservation of energy
Previous: Power
Question: A man lifts a  kg bucket from a well whose depth
is
kg bucket from a well whose depth
is  m. Assuming that the man lifts the bucket at a constant rate,
how much work does he perform?
m. Assuming that the man lifts the bucket at a constant rate,
how much work does he perform?
Answer: Let  be the mass of the bucket and
be the mass of the bucket and 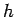 the depth of
the well. The gravitational force
the depth of
the well. The gravitational force 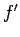 acting on the bucket is of magnitude
acting on the bucket is of magnitude  and
is directed vertically downwards. Hence,
and
is directed vertically downwards. Hence,  (where upward is defined to be positive).
The net upward displacement of the bucket is
(where upward is defined to be positive).
The net upward displacement of the bucket is 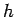 . Hence, the work
. Hence, the work 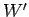 performed by the
gravitational force is the product of the (constant) force and the displacement of the
bucket along the line of action of that force:
performed by the
gravitational force is the product of the (constant) force and the displacement of the
bucket along the line of action of that force:
Note that 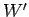 is negative, which implies that the gravitational field surrounding the
bucket gains energy as the bucket is lifted.
In order to lift the bucket at a constant rate, the man must exert a force
is negative, which implies that the gravitational field surrounding the
bucket gains energy as the bucket is lifted.
In order to lift the bucket at a constant rate, the man must exert a force 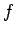 on the
bucket which balances (and very slightly exceeds) the force due to gravity.
Hence,
on the
bucket which balances (and very slightly exceeds) the force due to gravity.
Hence,  . It follows that the work
. It follows that the work 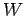 done by the man is
done by the man is
Note that the work is positive, which implies that the man expends energy whilst
lifting the bucket. Of course, since  , the energy expended by the
man equals the energy gained by the gravitational field.
, the energy expended by the
man equals the energy gained by the gravitational field.



Next: Worked example 5.2: Dragging
Up: Conservation of energy
Previous: Power
Richard Fitzpatrick
2006-02-02
![]() be the mass of the bucket and
be the mass of the bucket and ![]() the depth of
the well. The gravitational force
the depth of
the well. The gravitational force ![]() acting on the bucket is of magnitude
acting on the bucket is of magnitude ![]() and
is directed vertically downwards. Hence,
and
is directed vertically downwards. Hence, ![]() (where upward is defined to be positive).
The net upward displacement of the bucket is
(where upward is defined to be positive).
The net upward displacement of the bucket is ![]() . Hence, the work
. Hence, the work ![]() performed by the
gravitational force is the product of the (constant) force and the displacement of the
bucket along the line of action of that force:
performed by the
gravitational force is the product of the (constant) force and the displacement of the
bucket along the line of action of that force: