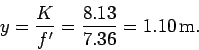Next: Worked example 5.6: Driving
Up: Conservation of energy
Previous: Worked example 5.4: Roller
Question: A block of mass  starts at rest at a height of
starts at rest at a height of
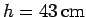 on a plane that has an angle of inclination of
on a plane that has an angle of inclination of
 with
respect to the horizontal. The block slides down the
plane, and, upon reaching the bottom, then slides along a horizontal
surface. The coefficient of kinetic friction of the block on both surfaces is
with
respect to the horizontal. The block slides down the
plane, and, upon reaching the bottom, then slides along a horizontal
surface. The coefficient of kinetic friction of the block on both surfaces is 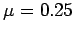 .
How far does the block slide along the horizontal surface before coming to rest?
.
How far does the block slide along the horizontal surface before coming to rest?
Answer:
The normal reaction of the plane to the block's weight is
Hence, the frictional force acting on the block when it is sliding down the plane
is
The change in gravitational potential energy of the block as it slides down the
plane is
The work 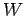 done on the block by the
frictional force during this process is
done on the block by the
frictional force during this process is
where
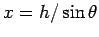 is the distance the block slides.
The minus sign indicates that
is the distance the block slides.
The minus sign indicates that 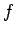 acts in the opposite direction to the displacement of the block.
Hence,
acts in the opposite direction to the displacement of the block.
Hence,
Now, by energy conservation, the kinetic energy 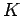 of the block at the bottom of the plane
equals the decrease in the block's potential energy plus the amount
of work done on the block:
of the block at the bottom of the plane
equals the decrease in the block's potential energy plus the amount
of work done on the block:
The frictional force acting on the block when it slides over the horizontal
surface is
The work done on the block as it slides a distance  over this
surface is
over this
surface is
By energy conservation, the block comes to rest when the action of the frictional force has
drained all of the kinetic energy from the block: i.e., when  . It follows
that
. It follows
that



Next: Worked example 5.6: Driving
Up: Conservation of energy
Previous: Worked example 5.4: Roller
Richard Fitzpatrick
2006-02-02