Worked example 4.2: Block accelerating up a slope

Question: Consider the diagram. Suppose that the block, mass $m= 5 {\rm kg}$, is subject to a horizontal force $F= 27 {\rm N}$. What is the acceleration of the block up the (frictionless) slope?

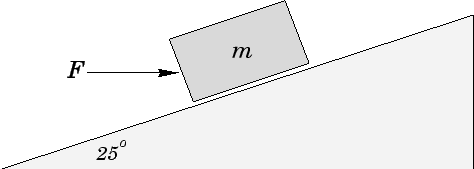
Answer: Only that component of the applied force which is parallel to the incline has any influence on the block's motion: the normal component of the applied force is canceled out by the normal reaction of the incline. The component of the applied force acting up the incline is $F \cos 25^\circ$. Likewise, the component of the block's weight acting down the incline is $m g \sin 25^\circ$. Hence, using Newton's second law to determine the acceleration $a$ of the block up the incline, we obtain

$$a = \frac{F \cos 25^\circ - m g \sin 25^\circ}{m}.$$

Since $m= 5 {\rm kg}$ and $F= 27 {\rm N}$, we have

$$a = \frac{27\times 0.9063 - 5\times 9.81\times 0.4226}{5} = 0.7483 {\rm m/s^2}.$$