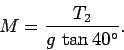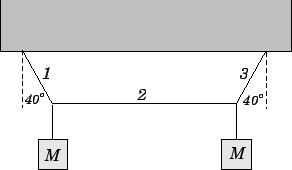

Answer: It follows from symmetry that the tensions in strings 1 and 3 are equal.
Let ![]() be the tension in string 1, and
be the tension in string 1, and ![]() the
tension in string 2. Consider the equilibrium of the knot above the leftmost mass.
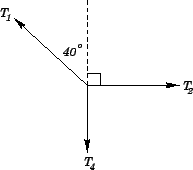
As shown below, this knot is subject to three forces: the downward force
the
tension in string 2. Consider the equilibrium of the knot above the leftmost mass.
As shown below, this knot is subject to three forces: the downward force ![]() due to the tension in the string which directly supports the leftmost mass, the rightward force
due to the tension in the string which directly supports the leftmost mass, the rightward force
![]() due to the tension in string 2, and the upward and leftward force
due to the tension in string 2, and the upward and leftward force
![]() due to the tension in string 1. The resultant of all these forces must be zero, otherwise
the system would not be in equilibrium. Resolving in the horizontal direction (with rightward
forces positive), we obtain
due to the tension in string 1. The resultant of all these forces must be zero, otherwise
the system would not be in equilibrium. Resolving in the horizontal direction (with rightward
forces positive), we obtain