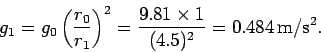Answer: Let ![]() be the Earth's radius. The distance of the rocket from the
centre of the Earth is
be the Earth's radius. The distance of the rocket from the
centre of the Earth is
![]() . We know that the free-fall
acceleration of the rocket when its distance from the Earth's centre is
. We know that the free-fall
acceleration of the rocket when its distance from the Earth's centre is ![]() (i.e., when it
is at the Earth's surface)
is
(i.e., when it
is at the Earth's surface)
is
![]() . Moreover, we know that gravity is an inverse-square law (i.e.,
. Moreover, we know that gravity is an inverse-square law (i.e.,
![]() ).
Hence, the rocket's acceleration is
).
Hence, the rocket's acceleration is