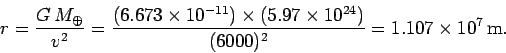

Next: Worked example 12.4: Halley's
Up: Orbital motion
Previous: Worked example 12.2: Acceleration
Question: A satellite moves in a circular orbit around the Earth with speed
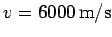 . Determine the satellite's altitude above the Earth's surface.
Determine the period of the satellite's orbit. The Earth's mass and radius are
. Determine the satellite's altitude above the Earth's surface.
Determine the period of the satellite's orbit. The Earth's mass and radius are
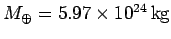 and
and
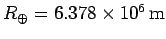 ,
respectively.
,
respectively.
Answer: The acceleration of the satellite towards the centre of the Earth
is 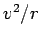 , where
, where 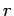 is its orbital radius. This acceleration must be provided by the
acceleration
is its orbital radius. This acceleration must be provided by the
acceleration
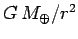 due to the Earth's gravitational attraction.
Hence,
due to the Earth's gravitational attraction.
Hence,
The above expression can be rearranged to give
Thus, the satellite's altitude above the Earth's surface is
The satellite's orbital period is simply
Richard Fitzpatrick
2006-02-02
![]() , where
, where ![]() is its orbital radius. This acceleration must be provided by the
acceleration
is its orbital radius. This acceleration must be provided by the
acceleration
![]() due to the Earth's gravitational attraction.
Hence,
due to the Earth's gravitational attraction.
Hence,