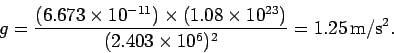Next: Worked example 12.2: Acceleration
Up: Orbital motion
Previous: Planetary orbits
Question: Callisto is the eighth of Jupiter's moons: its mass and radius are
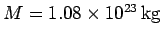 and
and
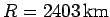 , respectively. What is the gravitational
acceleration on the surface
of this moon?
, respectively. What is the gravitational
acceleration on the surface
of this moon?
Answer: The surface gravitational acceleration on a spherical body of mass  and radius
and radius  is
simply
is
simply
Hence,
Richard Fitzpatrick
2006-02-02
![]() and radius
and radius ![]() is
simply
is
simply