


Next: Worked example 11.6: Oscillating
Up: Oscillatory motion
Previous: Worked example 11.4: Energy
Question: Having landed on a newly discovered planet, an astronaut sets up
a simple pendulum of length 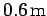 , and finds that it makes 51 complete
oscillations in 1 minute. The amplitude of the oscillations is small compared to the
length of the pendulum. What is the surface gravitational acceleration on the planet?
, and finds that it makes 51 complete
oscillations in 1 minute. The amplitude of the oscillations is small compared to the
length of the pendulum. What is the surface gravitational acceleration on the planet?
Answer: The frequency of the oscillations is
Hence, the angular frequency is
Now,
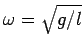 for small amplitude oscillations of a simple pendulum. Rearrangement off this formula gives
for small amplitude oscillations of a simple pendulum. Rearrangement off this formula gives
Hence, the surface gravitational acceleration is
 .
.
Richard Fitzpatrick
2006-02-02
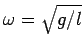 for small amplitude oscillations of a simple pendulum. Rearrangement off this formula gives
for small amplitude oscillations of a simple pendulum. Rearrangement off this formula gives