Next: Worked example 11.5: Gravity
Up: Oscillatory motion
Previous: Worked example 11.3: Block
Question:
A block of mass 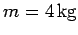 is attached to a spring, and undergoes simple harmonic
motion with a period of
is attached to a spring, and undergoes simple harmonic
motion with a period of
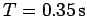 . The total energy of the system is
. The total energy of the system is
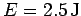 . What is the force constant of the spring? What is the amplitude
of the motion?
. What is the force constant of the spring? What is the amplitude
of the motion?
Answer:
The angular frequency of the motion is
Now,
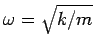 for a mass on a spring. Rearrangement of this formula yields
for a mass on a spring. Rearrangement of this formula yields
The total energy of a system executing simple harmonic motion is
 . Rearrangement of this formula gives
. Rearrangement of this formula gives
Thus, the force constant is
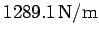 and the amplitude is
and the amplitude is
 .
.
Richard Fitzpatrick
2006-02-02
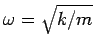 for a mass on a spring. Rearrangement of this formula yields
for a mass on a spring. Rearrangement of this formula yields