


Next: Orbital motion
Up: Oscillatory motion
Previous: Worked example 11.5: Gravity
Question: A uniform disk of radius
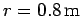 and mass
and mass
 is freely suspended from a horizontal pivot located a radial distance
is freely suspended from a horizontal pivot located a radial distance
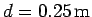 from its centre.
Find the angular frequency of small amplitude oscillations of the disk.
from its centre.
Find the angular frequency of small amplitude oscillations of the disk.
Answer: The moment of inertia of the disk about a perpendicular axis passing through its
centre is
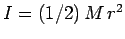 . From the parallel axis theorem, the moment of inertia of the disk
about the pivot point is
. From the parallel axis theorem, the moment of inertia of the disk
about the pivot point is
The angular frequency of small amplitude oscillations of a compound pendulum is given by
Hence, the answer is
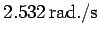 .
.
Richard Fitzpatrick
2006-02-02
![]() . From the parallel axis theorem, the moment of inertia of the disk
about the pivot point is
. From the parallel axis theorem, the moment of inertia of the disk
about the pivot point is
