Worked example 10.2: Rod supported by a cable

Question: A uniform rod of mass $m= 15 {\rm kg}$ and length $l=3 {\rm m}$ is supported in a horizontal position by a pin and a cable, as shown in the figure below. Masses $m_1=36 {\rm kg}$ and $m_2=24 {\rm kg}$ are suspended from the rod at positions $l_1=0.5 {\rm m}$ and $l_2=2.3 {\rm m}$. The angle $\theta$ is $40^\circ$. What is the tension $T$ in the cable?

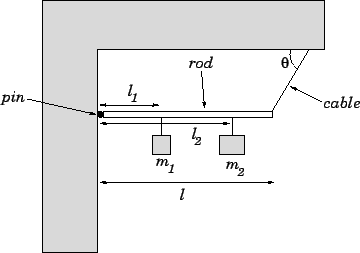
Answer: Consider the torque acting on the rod about the pin. Note that the reaction at the pin makes no contribution to this torque (since the length of the associated lever arm is zero). The torque due to the weight of the rod is $m g l/2$ (i.e., the weight times the length of the lever arm). Note that the weight of the rod acts at its centre of mass, which is located at the rod's mid-point. The torque due to the weight of the first mass is $m_1 g l_1$. The torque due to the weight of the second mass is $m_2 g l_2$. Finally, the torque due to the tension in the cable is $-T l \sin\theta$ (this torque is negative since it twists the rod in the opposite sense to the other three torques). Hence, setting the net torque to zero, we obtain

$$m g \frac{l}{2} + m_1 g l_1 + m_2 g l_2 -T l \sin\theta = 0,$$

or

$$T = \frac{ [m/2 + m_1 (l_1/l) + m_2 (l_2/l)] g }{\sin\theta}$$

$$= \frac{[0.5\times 15 + 36\times(0.5/3)+24\times(2.3/3)]\times 9.81}{\sin 40^\circ}$$

$$= 486.84 {\rm N}.$$