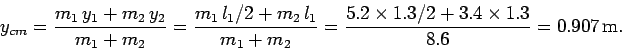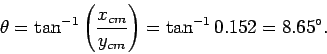Next: Worked example 10.2: Rod
Up: Statics
Previous: Jointed rods
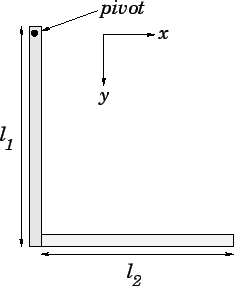
Question: Suppose that two uniform rods (of negligible thickness)
are welded together at right-angles, as shown in the
diagram below. Let the first rod be of mass
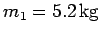 and length
and length
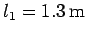 .
Let the second rod be of mass
.
Let the second rod be of mass
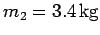 and length
and length
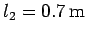 . Suppose that
the system is suspended from a pivot point located at the free end of the first rod, and then allowed to
reach a stable equilibrium state. What angle
. Suppose that
the system is suspended from a pivot point located at the free end of the first rod, and then allowed to
reach a stable equilibrium state. What angle  does the first rod subtend with the
downward vertical in this state?
does the first rod subtend with the
downward vertical in this state?
Answer: Let us adopt a coordinate system in which the  -axis runs
parallel to the second rod, whereas the
-axis runs
parallel to the second rod, whereas the  -axis runs parallel to the first. Let the origin
of our coordinate system correspond to the pivot point. The centre of mass
of the first rod is situated at its mid-point, whose coordinates are
-axis runs parallel to the first. Let the origin
of our coordinate system correspond to the pivot point. The centre of mass
of the first rod is situated at its mid-point, whose coordinates are
Likewise, the centre of mass of the second rod is situated at its mid-point, whose
coordinates are
It follows that the coordinates of the centre of mass of the whole system are
given by
and
The angle  subtended between the line joining the pivot point and the overall centre of mass,
and the first rod is simply
subtended between the line joining the pivot point and the overall centre of mass,
and the first rod is simply
When the system reaches a stable equilibrium state then its centre of mass is aligned
directly below the pivot point. This implies that the first rod
subtends an angle
 with the downward vertical.
with the downward vertical.



Next: Worked example 10.2: Rod
Up: Statics
Previous: Jointed rods
Richard Fitzpatrick
2006-02-02

![]() -axis runs
parallel to the second rod, whereas the
-axis runs
parallel to the second rod, whereas the ![]() -axis runs parallel to the first. Let the origin
of our coordinate system correspond to the pivot point. The centre of mass
of the first rod is situated at its mid-point, whose coordinates are
-axis runs parallel to the first. Let the origin
of our coordinate system correspond to the pivot point. The centre of mass
of the first rod is situated at its mid-point, whose coordinates are