Worked example 8.2: Accelerating a wheel

Question: The net work done in accelerating a wheel from rest to an angular speed of 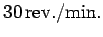$30 {\rm rev./min.}$ is $W=5500 {\rm J}$. What is the moment of inertia of the wheel?

Answer: The final angular speed of the wheel is

$$\omega = 30\times 2 \pi/60 = 3.142 {\rm rad./s}.$$

Assuming that all of the work 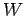$W$ performed on the wheel goes to increase its rotational kinetic energy, we have

$$W = \frac{1}{2} I \omega^2,$$

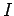where $I$ is the wheel's moment of inertia. It follows that

$$I = \frac{2 W}{\omega^2} = \frac{2\times 5500}{3.142^2}= 1114.6 {\rm kg m^2}.$$