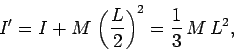Next: Worked example 8.4: Weight
Up: Rotational motion
Previous: Worked example 8.2: Accelerating
Question: A rod of mass 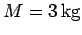 and length
and length
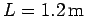 pivots
about an axis, perpendicular to its length, which passes through one of its ends. What
is the moment of inertia of the rod? Given that the rod's instantaneous angular velocity is
pivots
about an axis, perpendicular to its length, which passes through one of its ends. What
is the moment of inertia of the rod? Given that the rod's instantaneous angular velocity is
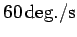 , what is its rotational kinetic energy?
, what is its rotational kinetic energy?
Answer: The moment of inertia of a rod of mass 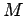 and length
and length 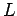 about
an axis, perpendicular to its length, which passes through its midpoint is
about
an axis, perpendicular to its length, which passes through its midpoint is
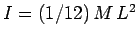 . This is a standard result.
Using the parallel axis theorem, the moment of inertia
about a parallel axis passing through one of the ends of the rod
is
. This is a standard result.
Using the parallel axis theorem, the moment of inertia
about a parallel axis passing through one of the ends of the rod
is
so
The instantaneous angular velocity of the rod is
Hence, the rod's rotational kinetic energy is written



Next: Worked example 8.4: Weight
Up: Rotational motion
Previous: Worked example 8.2: Accelerating
Richard Fitzpatrick
2006-02-02
![]() and length
and length ![]() about
an axis, perpendicular to its length, which passes through its midpoint is
about
an axis, perpendicular to its length, which passes through its midpoint is
![]() . This is a standard result.
Using the parallel axis theorem, the moment of inertia
about a parallel axis passing through one of the ends of the rod
is
. This is a standard result.
Using the parallel axis theorem, the moment of inertia
about a parallel axis passing through one of the ends of the rod
is