


Next: Worked example 8.2: Accelerating
Up: Rotational motion
Previous: Combined translational and rotational
Question: A tire placed on a balancing machine in a
service station starts from rest and turns through 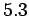 revolutions
in
revolutions
in 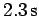 before reaching its final angular speed. What is the
angular acceleration of the tire (assuming that this quantity remains constant)?
What is the final angular speed of the tire?
before reaching its final angular speed. What is the
angular acceleration of the tire (assuming that this quantity remains constant)?
What is the final angular speed of the tire?
Answer: The tire turns through
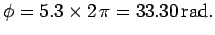 in
in
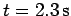 . The relationship between
. The relationship between 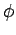 and
and  for the case of rotational
motion, starting from
rest,
with uniform angular acceleration
for the case of rotational
motion, starting from
rest,
with uniform angular acceleration 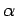 is
is
Hence,
Given that the tire starts from rest, its angular velocity after  seconds takes the form
seconds takes the form
Richard Fitzpatrick
2006-02-02
![]() in
in
![]() . The relationship between
. The relationship between ![]() and
and ![]() for the case of rotational
motion, starting from
rest,
with uniform angular acceleration
for the case of rotational
motion, starting from
rest,
with uniform angular acceleration ![]() is
is
![]() seconds takes the form
seconds takes the form