There is, of course, no way in which a block can slide over a frictional surface without dissipating energy. However, we know from experience that a round object can roll over such a surface with hardly any dissipation. For instance, it is far easier to drag a heavy suitcase across the concourse of an airport if the suitcase has wheels on the bottom. Let us investigate the physics of round objects rolling over rough surfaces, and, in particular, rolling down rough inclines.
Consider a uniform cylinder of radius ![]() rolling over a horizontal, frictional surface.
See Fig. 83. Let
rolling over a horizontal, frictional surface.
See Fig. 83. Let ![]() be the translational velocity of the cylinder's centre of
mass, and let
be the translational velocity of the cylinder's centre of
mass, and let ![]() be the angular velocity of the cylinder about an axis running along
its length, and passing through its centre of mass. Consider the point
of contact between the cylinder and the surface. The velocity
be the angular velocity of the cylinder about an axis running along
its length, and passing through its centre of mass. Consider the point
of contact between the cylinder and the surface. The velocity ![]() of this point
is made up of two components: the translational velocity
of this point
is made up of two components: the translational velocity ![]() , which is common to all
elements of the cylinder, and the tangential velocity
, which is common to all
elements of the cylinder, and the tangential velocity
![]() , due to the
cylinder's rotational motion. Thus,
, due to the
cylinder's rotational motion. Thus,
| (396) |
Consider, now, what happens when the cylinder shown in Fig. 83 rolls,
without slipping, down a rough slope whose angle of inclination, with respect to the horizontal, is
![]() . If the cylinder starts from rest, and rolls down the slope a vertical distance
. If the cylinder starts from rest, and rolls down the slope a vertical distance
![]() , then its gravitational potential energy decreases by
, then its gravitational potential energy decreases by
![]() ,
where
,
where ![]() is the mass of the cylinder. This decrease in potential energy must be
offset by a corresponding increase in kinetic energy. (Recall that when a
cylinder rolls without slipping there is no frictional energy loss.) However, a rolling
cylinder can possesses two different types of kinetic energy. Firstly, translational
kinetic energy:
is the mass of the cylinder. This decrease in potential energy must be
offset by a corresponding increase in kinetic energy. (Recall that when a
cylinder rolls without slipping there is no frictional energy loss.) However, a rolling
cylinder can possesses two different types of kinetic energy. Firstly, translational
kinetic energy:
![]() , where
, where ![]() is the cylinder's translational
velocity; and, secondly, rotational kinetic energy:
is the cylinder's translational
velocity; and, secondly, rotational kinetic energy:
![]() , where
, where ![]() is the cylinder's angular velocity, and
is the cylinder's angular velocity, and ![]() is its moment of inertia. Hence,
energy conservation yields
is its moment of inertia. Hence,
energy conservation yields
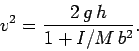 |
(399) |
Let us examine the equations of motion of a cylinder, of mass ![]() and radius
and radius ![]() , rolling down a
rough slope without slipping. As shown in Fig. 84, there are three
forces acting on the cylinder. Firstly, we have the cylinder's weight,
, rolling down a
rough slope without slipping. As shown in Fig. 84, there are three
forces acting on the cylinder. Firstly, we have the cylinder's weight, ![]() , which acts
vertically downwards. Secondly, we have the reaction,
, which acts
vertically downwards. Secondly, we have the reaction, ![]() , of the slope, which acts
normally outwards from the surface of the slope. Finally, we have the frictional force,
, of the slope, which acts
normally outwards from the surface of the slope. Finally, we have the frictional force, ![]() ,
which acts up the slope, parallel to its surface.
,
which acts up the slope, parallel to its surface.
As we have already discussed, we can most easily describe the translational
motion of an extended body by following the motion of its centre of mass.
This motion is equivalent to that of a point particle, whose mass equals that
of the body, which is subject to the same external forces as those that act
on the body. Thus, applying the three forces, ![]() ,
, ![]() , and
, and ![]() , to
the cylinder's centre of mass, and resolving in the direction normal to the surface of the
slope, we obtain
, to
the cylinder's centre of mass, and resolving in the direction normal to the surface of the
slope, we obtain
| (402) |
Let us, now, examine the cylinder's rotational equation of motion.
First, we must evaluate the torques associated with the three forces
acting on the cylinder. Recall, that the torque associated with
a given force is the product of the magnitude of that force and the
length of the level arm--i.e., the
perpendicular distance between the line of action of the force and the
axis of rotation. Now, by definition, the weight of an extended
object acts at its centre of mass. However, in this case, the axis of
rotation passes through the centre of mass. Hence, the length of the lever
arm associated with the weight ![]() is zero. It follows
that the associated torque is also zero. It is clear, from Fig. 84, that
the line of action of the reaction force,
is zero. It follows
that the associated torque is also zero. It is clear, from Fig. 84, that
the line of action of the reaction force, ![]() , passes through the centre
of mass of the cylinder, which coincides with the axis of rotation.
Thus, the length of the lever
arm associated with
, passes through the centre
of mass of the cylinder, which coincides with the axis of rotation.
Thus, the length of the lever
arm associated with ![]() is zero, and so is the associated torque.
Finally, according to Fig. 84, the perpendicular distance between the line
of action of the friction force,
is zero, and so is the associated torque.
Finally, according to Fig. 84, the perpendicular distance between the line
of action of the friction force, ![]() , and the axis of rotation is just
the radius of the cylinder,
, and the axis of rotation is just
the radius of the cylinder, ![]() --so the associated torque is
--so the associated torque is ![]() .
We conclude that the net torque acting on the
cylinder is simply
.
We conclude that the net torque acting on the
cylinder is simply
| (404) |
Now, if the cylinder rolls, without slipping, such that the constraint (397)
is satisfied at all times, then the time derivative of this constraint implies the
following relationship between the cylinder's translational and rotational accelerations:
| (406) |
| (409) |
Now, in order for the slope to exert the frictional force specified in Eq. (410),
without any slippage between the slope and cylinder, this force must
be less than the maximum allowable static frictional force,
![]() , where
, where ![]() is
the coefficient of static friction. In other words, the condition for the
cylinder to roll down the slope without slipping is
is
the coefficient of static friction. In other words, the condition for the
cylinder to roll down the slope without slipping is ![]() , or
, or
| (411) |
Suppose, finally, that we place two cylinders, side by side and at rest, at the top of a
frictional slope
of inclination ![]() . Let the two cylinders possess the same mass,
. Let the two cylinders possess the same mass, ![]() , and the
same radius,
, and the
same radius, ![]() . However, suppose that the first cylinder is uniform, whereas the
second is a hollow shell. Which cylinder reaches the bottom of the slope first, assuming that they are
both released simultaneously, and both roll without slipping?
The acceleration of each cylinder down the slope is given by Eq. (407).
For the case of the solid cylinder, the moment of inertia is
. However, suppose that the first cylinder is uniform, whereas the
second is a hollow shell. Which cylinder reaches the bottom of the slope first, assuming that they are
both released simultaneously, and both roll without slipping?
The acceleration of each cylinder down the slope is given by Eq. (407).
For the case of the solid cylinder, the moment of inertia is
![]() ,
and so
,
and so
| (412) |
| (413) |