The existence of a ``sweet spot'' on a baseball bat is just a consequence of rotational dynamics.
Let us analyze this problem. Consider the schematic baseball bat shown in Fig. 82. Let ![]() be the mass of the bat, and let
be the mass of the bat, and let ![]() be its length. Suppose that the bat pivots about a fixed
point located at one of its ends. Let the centre of mass of the bat be located a
distance
be its length. Suppose that the bat pivots about a fixed
point located at one of its ends. Let the centre of mass of the bat be located a
distance ![]() from the pivot point. Finally, suppose that the ball strikes the
bat a distance
from the pivot point. Finally, suppose that the ball strikes the
bat a distance ![]() from the pivot point.
from the pivot point.
The collision between the bat and the ball can be modeled as equal and opposite impulses, ![]() ,
applied to each object at the time of the collision (see Sect. 6.5). At the same time,
equal and opposite impulses
,
applied to each object at the time of the collision (see Sect. 6.5). At the same time,
equal and opposite impulses ![]() are applied to the pivot and the bat,
as shown in Fig. 82. If the pivot actually corresponds to
a hitter's hands then the latter
impulse gives rise to the painful jarring sensation felt when the ball is not struck
properly.
are applied to the pivot and the bat,
as shown in Fig. 82. If the pivot actually corresponds to
a hitter's hands then the latter
impulse gives rise to the painful jarring sensation felt when the ball is not struck
properly.
We saw earlier that in a general multi-component system--which includes an extended
body such as a baseball bat--the motion of the
centre of mass takes a particularly simple form (see Sect. 6.3).
To be more exact, the motion of the centre of mass is equivalent to that
of the point particle obtained by concentrating the whole mass of the system at the centre of mass, and
then
allowing all of the external forces acting on the system to act upon that mass. Let us
use this idea to analyze the effect of the collision with the ball on the motion
of the bat's centre of mass. The centre of mass of the bat acts like a
point particle of mass ![]() which is subject to the two impulses,
which is subject to the two impulses, ![]() and
and ![]() (which
are applied simultaneously). If
(which
are applied simultaneously). If ![]() is the instantaneous velocity of the centre
of mass then the change in momentum of this point due to the action
of the two impulses is simply
is the instantaneous velocity of the centre
of mass then the change in momentum of this point due to the action
of the two impulses is simply
Note that in order to specify the instantaneous state of an extended body we must do more than just specify the location of the body's centre of mass. Indeed, since the body can rotate about its centre of mass, we must also specify its orientation in space. Thus, in order to follow the motion of an extended body, we must not only follow the translational motion of its centre of mass, but also the body's rotational motion about this point (or any other convenient reference point located within the body).
Consider the rotational motion of the bat shown in Fig. 82 about a perpendicular
(to the bat) axis passing through the pivot point. This motion satisfies
| (385) |
Now, the torque associated with a given force is equal to the magnitude of the force times the
length of the lever arm. Thus, it stands to reason that the angular impulse, ![]() , associated
with an impulse,
, associated
with an impulse, ![]() , is simply
, is simply
| (387) |
Now, the relationship between the instantaneous velocity of the bat's centre of mass
and the bat's instantaneous angular velocity is simply
| (389) |
Equations (388) and (390) can be combined to yield
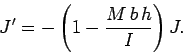 |
(391) |
Let us crudely model the bat as a uniform rod of length ![]() and
mass
and
mass ![]() . It follows, by symmetry, that the centre of mass of the bat
lies at its half-way point: i.e.,
. It follows, by symmetry, that the centre of mass of the bat
lies at its half-way point: i.e.,
| (392) |
| (393) |
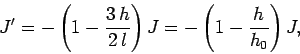 |
(394) |
| (395) |