


Next: Rocket science
Up: Conservation of momentum
Previous: Two-component systems
Multi-component systems
Figure 48:
A 3-dimensional dynamical system consisting of many point mass objects.
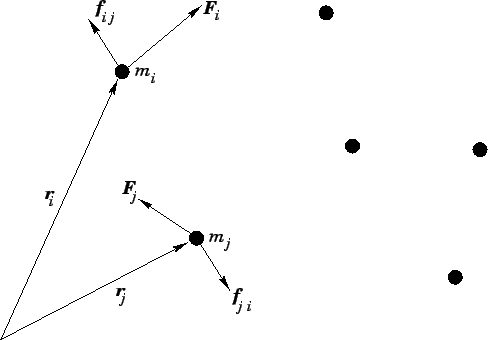 |
Consider a system of 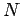 mutually interacting point mass objects which move in 3-dimensions.
See Fig. 48.
Let the
mutually interacting point mass objects which move in 3-dimensions.
See Fig. 48.
Let the 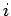 th object, whose mass is
th object, whose mass is 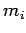 , be located at vector displacement
, be located at vector displacement 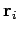 .
Suppose that this object exerts a force
.
Suppose that this object exerts a force 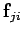 on the
on the 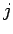 th object. By Newton's third
law of motion, the force
th object. By Newton's third
law of motion, the force 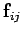 exerted by the
exerted by the 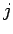 th object on the
th object on the 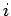 th is
given by
th is
given by
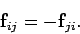 |
(195) |
Finally, suppose that the 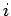 th object is subject to an external force
th object is subject to an external force 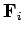 .
.
Newton's second law of motion applied to the 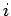 th object yields
th object yields
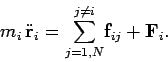 |
(196) |
Note that the summation on the right-hand side of the above equation excludes the case
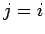 , since the
, since the 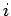 th object cannot exert a force on itself. Let us now take the above
equation and sum it over all objects. We obtain
th object cannot exert a force on itself. Let us now take the above
equation and sum it over all objects. We obtain
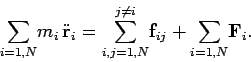 |
(197) |
Consider the sum over all internal forces: i.e., the first term on the right-hand side.
Each element of this sum--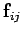 , say--can be paired with another element--
, say--can be paired with another element--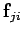 ,
in this case--which is equal and opposite. In other words,
the elements of the sum all cancel out in pairs. Thus, the net value of the sum is zero.
It follows that the above equation can be written
,
in this case--which is equal and opposite. In other words,
the elements of the sum all cancel out in pairs. Thus, the net value of the sum is zero.
It follows that the above equation can be written
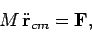 |
(198) |
where
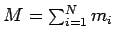 is the total mass, and
is the total mass, and
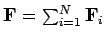 is the
net external force. The quantity
is the
net external force. The quantity 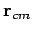 is the vector displacement of the centre of mass.
As before, the centre of mass is an imaginary point whose coordinates are the mass weighted
averages of the coordinates of the objects which constitute the system. Thus,
is the vector displacement of the centre of mass.
As before, the centre of mass is an imaginary point whose coordinates are the mass weighted
averages of the coordinates of the objects which constitute the system. Thus,
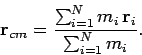 |
(199) |
According to Eq. (198), the motion of the centre of mass is equivalent to that which
would be obtained if all the mass contained in the system were collected at the centre of mass, and
this conglomerate mass were then acted upon by the net external force. As before, the motion
of the centre of mass is likely to be far simpler than the motions of the component masses.
Suppose that there is zero net external force acting on the system, so that
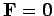 .
In this case, Eq. (198) implies that the centre of mass moves with uniform
velocity in a straight-line. In other words, the velocity of the centre of mass,
.
In this case, Eq. (198) implies that the centre of mass moves with uniform
velocity in a straight-line. In other words, the velocity of the centre of mass,
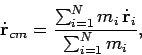 |
(200) |
is a constant of the motion. Now, the momentum of the  th object takes the
form
th object takes the
form
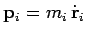 . Hence, the total momentum of the
system is written
. Hence, the total momentum of the
system is written
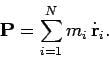 |
(201) |
A comparison of Eqs. (200) and (201) suggests that 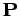 is also
a constant of the motion when zero net external force acts on the system. Finally,
Eq. (198) can be rewritten
is also
a constant of the motion when zero net external force acts on the system. Finally,
Eq. (198) can be rewritten
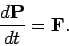 |
(202) |
In other words, the time derivative of the total momentum
is equal to the net external force acting on the system.
It is clear, from the above discussion, that most of the important results obtained in the
previous section, for the case of a two-component system moving
in 1-dimension, also apply to a multi-component system moving in 3-dimensions.
Figure 49:
The unfortunate history of the planet Krypton.
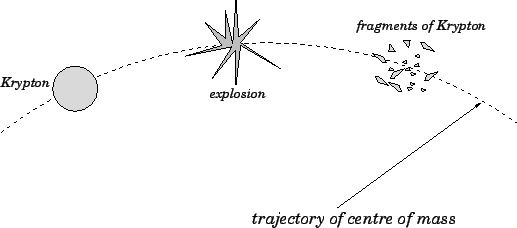 |
As an illustration of the points raised in the above discussion, let us consider the unfortunate
history of the planet Krypton. As you probably all know, Krypton--Superman's home planet--eventually
exploded.
Note, however, that before, during, and after this explosion the net external force acting
on Krypton, or the fragments of Krypton--namely, the gravitational attraction to Krypton's sun--remained
the same. In other words, the forces responsible for the explosion can be thought of as
large, transitory, internal forces. We conclude that the motion of the centre of mass of
Krypton, or the fragments of Krypton, was unaffected by the explosion. This follows, from
Eq. (198), since the motion of the centre of mass is independent of internal forces.
Before the explosion, the planet Krypton presumably executed a standard elliptical orbit
around Krypton's sun. We conclude that,
after the explosion, the fragments of Krypton (or, to be more exact, the
centre of mass of these fragments) continued to execute exactly the same orbit. See
Fig. 49.



Next: Rocket science
Up: Conservation of momentum
Previous: Two-component systems
Richard Fitzpatrick
2006-02-02

![]() mutually interacting point mass objects which move in 3-dimensions.
See Fig. 48.
Let the
mutually interacting point mass objects which move in 3-dimensions.
See Fig. 48.
Let the ![]() th object, whose mass is
th object, whose mass is ![]() , be located at vector displacement
, be located at vector displacement ![]() .
Suppose that this object exerts a force
.
Suppose that this object exerts a force ![]() on the
on the ![]() th object. By Newton's third
law of motion, the force
th object. By Newton's third
law of motion, the force ![]() exerted by the
exerted by the ![]() th object on the
th object on the ![]() th is
given by
th is
given by
![]() th object yields
th object yields
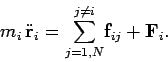
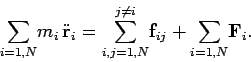
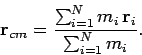
![]() .
In this case, Eq. (198) implies that the centre of mass moves with uniform
velocity in a straight-line. In other words, the velocity of the centre of mass,
.
In this case, Eq. (198) implies that the centre of mass moves with uniform
velocity in a straight-line. In other words, the velocity of the centre of mass,