


Next: Impulses
Up: Conservation of momentum
Previous: Multi-component systems
Figure 50:
A rocket.
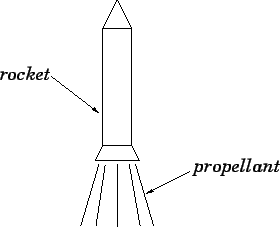 |
A rocket engine is the only type of propulsion device that operates
effectively in outer space. As shown in Fig. 50, a rocket works by ejecting a propellant at
high velocity from its rear end. The rocket exerts a backward force on the
propellant, in order to eject it, and, by Newton's third law, the propellant
exerts an equal and opposite force on the rocket, which propels it forward.
Let us attempt to find the equation of motion of a rocket. Let 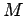 be the fixed mass of the
rocket engine and the payload, and
be the fixed mass of the
rocket engine and the payload, and 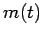 the total mass of the propellant contained
in the rocket's fuel tanks at time
the total mass of the propellant contained
in the rocket's fuel tanks at time 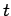 . Suppose that the rocket engine ejects the propellant
at some fixed velocity
. Suppose that the rocket engine ejects the propellant
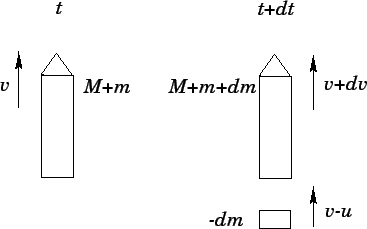
at some fixed velocity 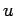 relative to the rocket. Let us examine the rocket at two
closely spaced instances in time. Suppose that at time
relative to the rocket. Let us examine the rocket at two
closely spaced instances in time. Suppose that at time 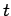 the rocket and propellant, whose
total mass is
the rocket and propellant, whose
total mass is 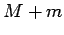 , are traveling with instantaneous velocity
, are traveling with instantaneous velocity 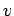 . Suppose, further, that
between times
. Suppose, further, that
between times 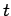 and
and 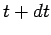 the rocket ejects a quantity of propellant of mass
the rocket ejects a quantity of propellant of mass 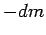 (n.b.,
(n.b., 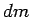 is understood to be negative,
so this represents a positive mass) which travels with velocity
is understood to be negative,
so this represents a positive mass) which travels with velocity 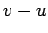 (i.e., velocity
(i.e., velocity
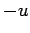 in the instantaneous rest frame of the rocket). As a result of the fuel
ejection, the velocity of the rocket
at time
in the instantaneous rest frame of the rocket). As a result of the fuel
ejection, the velocity of the rocket
at time 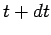 is boosted to
is boosted to 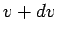 , and its total
mass becomes
, and its total
mass becomes 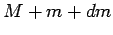 . See Fig. 51.
. See Fig. 51.
Figure 51:
Derivation of the rocket equation.
 |
Now, there is zero external force acting on the system, since the rocket is assumed to be in outer space.
It follows that the total momentum of the system is a constant of the motion. Hence, we
can equate the momenta evaluated at times 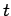 and
and 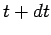 :
:
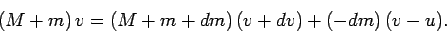 |
(203) |
Neglecting second order quantities (i.e., 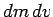 ), the above expression
yields
), the above expression
yields
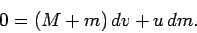 |
(204) |
Rearranging, we obtain
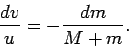 |
(205) |
Let us integrate the above equation between an initial time at which the rocket is
fully fueled--i.e., 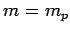 , where
, where 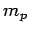 is the maximum mass of propellant that the
rocket can carry--but stationary, and a final time at which the mass of the fuel is
is the maximum mass of propellant that the
rocket can carry--but stationary, and a final time at which the mass of the fuel is 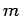 and the velocity of the rocket is
and the velocity of the rocket is 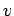 . Hence,
. Hence,
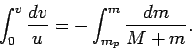 |
(206) |
It follows that
![\begin{displaymath}
\left[\frac{v}{u}\right]_{v=0}^{v=v}= -\left[\ln(M+m)\right]_{m=m_p}^{m=m},
\end{displaymath}](img874.png) |
(207) |
which yields
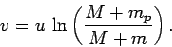 |
(208) |
The final velocity of the rocket (i.e., the velocity attained by the time
the rocket has exhausted its fuel, so that 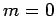 ) is
) is
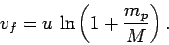 |
(209) |
Note that, unless the initial mass of the fuel exceeds the fixed mass of the
rocket by many orders of magnitude
(which is highly unlikely), the final velocity 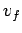 of the rocket is similar to
the velocity
of the rocket is similar to
the velocity 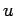 with which fuel is ejected from the rear of the rocket in
its instantaneous rest frame. This follows because
with which fuel is ejected from the rear of the rocket in
its instantaneous rest frame. This follows because
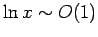 , unless
, unless  becomes
extremely large.
becomes
extremely large.
Let us now consider the factors which might influence the design of a rocket for use in interplanetary or
interstellar travel. Since the distances involved in such travel are vast, it is
important that the rocket's final velocity be made as large as possible, otherwise the journey
is going to take an unacceptably long time. However, as we have just seen, the factor which
essentially determines the final velocity 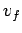 of a rocket is the speed of ejection
of a rocket is the speed of ejection 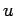 of
the propellant relative to the rocket. Broadly speaking,
of
the propellant relative to the rocket. Broadly speaking, 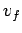 can never significantly
exceed
can never significantly
exceed 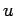 . It follows that a rocket suitable for interplanetary or
interstellar travel should have as high an ejection speed as practically possible.
Now, ordinary chemical rockets (the kind which powered the Apollo moon program)
can develop enormous thrusts, but are limited to ejection velocities below
about
. It follows that a rocket suitable for interplanetary or
interstellar travel should have as high an ejection speed as practically possible.
Now, ordinary chemical rockets (the kind which powered the Apollo moon program)
can develop enormous thrusts, but are limited to ejection velocities below
about
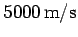 . Such rockets are ideal for lifting payloads out of the Earth's
gravitational field, but their relatively low ejection velocities render them unsuitable for
long distance space travel. A new type of rocket engine, called an ion thruster, is currently
under development: ion thrusters operate by accelerating ions electrostatically to great
velocities, and then ejecting them. Although ion thrusters only generate very small thrusts, compared to
chemical rockets, their much larger ejection velocities (up to 100 times those
of chemical rockets) makes them far more suitable for interplanetary or interstellar space travel.
The first spacecraft to employ an ion thruster was the
Deep Space 1 probe, which was launched from Cape Canaveral on October 24, 1998: this
probe successfully encountered the asteroid 9969 Braille in July, 1999.
. Such rockets are ideal for lifting payloads out of the Earth's
gravitational field, but their relatively low ejection velocities render them unsuitable for
long distance space travel. A new type of rocket engine, called an ion thruster, is currently
under development: ion thrusters operate by accelerating ions electrostatically to great
velocities, and then ejecting them. Although ion thrusters only generate very small thrusts, compared to
chemical rockets, their much larger ejection velocities (up to 100 times those
of chemical rockets) makes them far more suitable for interplanetary or interstellar space travel.
The first spacecraft to employ an ion thruster was the
Deep Space 1 probe, which was launched from Cape Canaveral on October 24, 1998: this
probe successfully encountered the asteroid 9969 Braille in July, 1999.



Next: Impulses
Up: Conservation of momentum
Previous: Multi-component systems
Richard Fitzpatrick
2006-02-02

![]() be the fixed mass of the
rocket engine and the payload, and
be the fixed mass of the
rocket engine and the payload, and ![]() the total mass of the propellant contained
in the rocket's fuel tanks at time
the total mass of the propellant contained
in the rocket's fuel tanks at time ![]() . Suppose that the rocket engine ejects the propellant
at some fixed velocity
. Suppose that the rocket engine ejects the propellant
at some fixed velocity ![]() relative to the rocket. Let us examine the rocket at two
closely spaced instances in time. Suppose that at time
relative to the rocket. Let us examine the rocket at two
closely spaced instances in time. Suppose that at time ![]() the rocket and propellant, whose
total mass is
the rocket and propellant, whose
total mass is ![]() , are traveling with instantaneous velocity
, are traveling with instantaneous velocity ![]() . Suppose, further, that
between times
. Suppose, further, that
between times ![]() and
and ![]() the rocket ejects a quantity of propellant of mass
the rocket ejects a quantity of propellant of mass ![]() (n.b.,
(n.b., ![]() is understood to be negative,
so this represents a positive mass) which travels with velocity
is understood to be negative,
so this represents a positive mass) which travels with velocity ![]() (i.e., velocity
(i.e., velocity
![]() in the instantaneous rest frame of the rocket). As a result of the fuel
ejection, the velocity of the rocket
at time
in the instantaneous rest frame of the rocket). As a result of the fuel
ejection, the velocity of the rocket
at time ![]() is boosted to
is boosted to ![]() , and its total
mass becomes
, and its total
mass becomes ![]() . See Fig. 51.
. See Fig. 51.
![]() and
and ![]() :
:
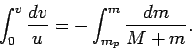
![]() of a rocket is the speed of ejection
of a rocket is the speed of ejection ![]() of
the propellant relative to the rocket. Broadly speaking,
of
the propellant relative to the rocket. Broadly speaking, ![]() can never significantly
exceed
can never significantly
exceed ![]() . It follows that a rocket suitable for interplanetary or
interstellar travel should have as high an ejection speed as practically possible.
Now, ordinary chemical rockets (the kind which powered the Apollo moon program)
can develop enormous thrusts, but are limited to ejection velocities below
about
. It follows that a rocket suitable for interplanetary or
interstellar travel should have as high an ejection speed as practically possible.
Now, ordinary chemical rockets (the kind which powered the Apollo moon program)
can develop enormous thrusts, but are limited to ejection velocities below
about
![]() . Such rockets are ideal for lifting payloads out of the Earth's
gravitational field, but their relatively low ejection velocities render them unsuitable for
long distance space travel. A new type of rocket engine, called an ion thruster, is currently
under development: ion thrusters operate by accelerating ions electrostatically to great
velocities, and then ejecting them. Although ion thrusters only generate very small thrusts, compared to
chemical rockets, their much larger ejection velocities (up to 100 times those
of chemical rockets) makes them far more suitable for interplanetary or interstellar space travel.
The first spacecraft to employ an ion thruster was the
Deep Space 1 probe, which was launched from Cape Canaveral on October 24, 1998: this
probe successfully encountered the asteroid 9969 Braille in July, 1999.
. Such rockets are ideal for lifting payloads out of the Earth's
gravitational field, but their relatively low ejection velocities render them unsuitable for
long distance space travel. A new type of rocket engine, called an ion thruster, is currently
under development: ion thrusters operate by accelerating ions electrostatically to great
velocities, and then ejecting them. Although ion thrusters only generate very small thrusts, compared to
chemical rockets, their much larger ejection velocities (up to 100 times those
of chemical rockets) makes them far more suitable for interplanetary or interstellar space travel.
The first spacecraft to employ an ion thruster was the
Deep Space 1 probe, which was launched from Cape Canaveral on October 24, 1998: this
probe successfully encountered the asteroid 9969 Braille in July, 1999.