


Next: Example Eclipse Calculations
Up: Lunar-Solar Syzygies and Eclipses
Previous: Example Syzygy Calculations
A solar eclipse--or, more accurately, a lunar-solar occultation--occurs
when the moon blocks the light of the sun. Clearly, this is
only possible at a new moon--see Fig. 26. On the other hand,
a lunar eclipse occurs when the moon falls into the
shadow of the earth. Of course, this is only possible at a full moon. It follows that eclipses
can only take place at lunar-solar syzygies.
In order to determine whether a particular lunar-solar syzygy conincides with an eclipse, we first need to calculate the angular radii of the
sun, the moon, and the earth's shadow in the sky. Using the small angle approximation, the
angular radius of the sun is given by
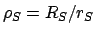 , where
, where
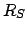 is the solar radius, and
is the solar radius, and 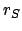 the earth-sun distance. However,
the earth-sun distance. However,
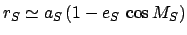 , where
, where 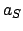 ,
, 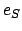 , and
, and 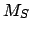 are the major radius, eccentricity, and mean anomaly of the sun's apparent
orbit around the earth, respectively (see Cha. 4). Hence,
are the major radius, eccentricity, and mean anomaly of the sun's apparent
orbit around the earth, respectively (see Cha. 4). Hence,
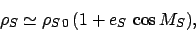 |
(140) |
where
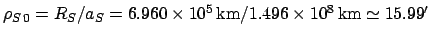 .
Likewise, the angular radius of the moon is
.
Likewise, the angular radius of the moon is
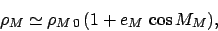 |
(141) |
where
 . Here,
. Here,
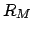 ,
,  ,
, 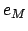 , and
, and  are the radius of the moon, and the major radius, eccentricity, and mean anomaly of the moon's orbit, respectively.
As was shown in the previous chapter, lunar parallax causes the
angular position of the moon in the sky to shift by up to
are the radius of the moon, and the major radius, eccentricity, and mean anomaly of the moon's orbit, respectively.
As was shown in the previous chapter, lunar parallax causes the
angular position of the moon in the sky to shift by up to
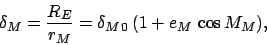 |
(142) |
where
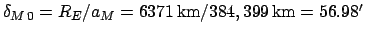 . Here,
. Here, 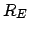 is the
radius of the earth. Finally, simple trigonometry reveals that
the angular size of the earth's shadow (i.e., umbra) at the radius of the moon's orbit is
is the
radius of the earth. Finally, simple trigonometry reveals that
the angular size of the earth's shadow (i.e., umbra) at the radius of the moon's orbit is
 |
(143) |
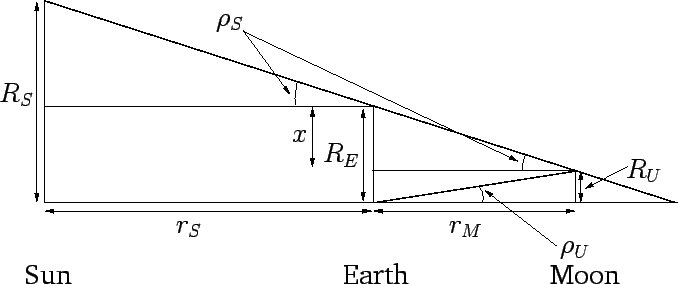
This can be seen from Fig. 27.
The radius of the umbra at the position of the moon is
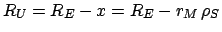 . Hence, the angular radius of the umbra is
. Hence, the angular radius of the umbra is
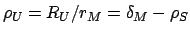 . Incidentally,
the identification of two of the angles in the figure with
. Incidentally,
the identification of two of the angles in the figure with
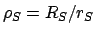 follows
because
follows
because 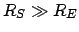 .
.
Figure 27:
The earth's umbra.
 |
A solar eclipse does not take place every new moon,
nor a lunar eclipse every full moon, because of the inclination of the
moon's orbit to the ecliptic plane, which causes the moon to
pass either above or below the sun, or the earth's shadow, respectively, in the majority of cases. It follows
that the critical parameter which determines the occurrence of eclipses is
the ecliptic latitude of the moon at syzygy, 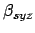 . Of course, once
the date and time of a syzygy has been established,
. Of course, once
the date and time of a syzygy has been established, 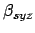 can be calculated from Table 38. However, the lunar argument of latitude,
can be calculated from Table 38. However, the lunar argument of latitude, 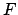 , must first be determined using
, must first be determined using
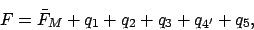 |
(144) |
where 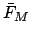 comes from Table 40,
comes from Table 40, 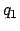 ,
, 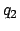 ,
,  , and
, and 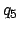 are obtained from Table 41,
and
are obtained from Table 41,
and 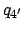 is the
is the  from Table 37. For instance, we
have seen that for the third new moon of 1982 CE,
from Table 37. For instance, we
have seen that for the third new moon of 1982 CE,
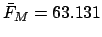 ,
,
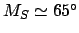 ,
,
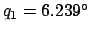 ,
,
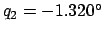 ,
,
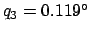 , and
, and
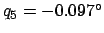 . According to Table 37,
. According to Table 37,
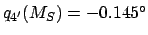 . Hence,
. Hence,
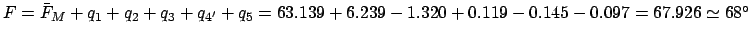 .
It follows from Table 38 that
.
It follows from Table 38 that
 .
.
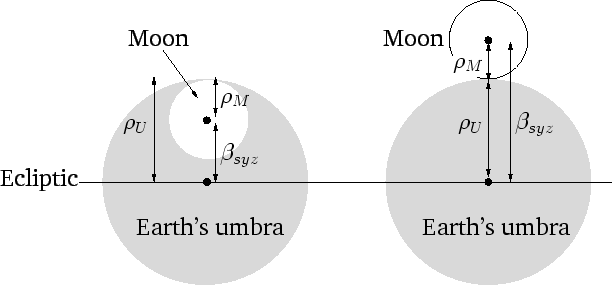
Figure 28:
The limiting cases for a total lunar eclipse (left) and a partial lunar eclipse (right).
 |
The criterion for
a lunar eclipse is particularly simple, since it is not
complicated by lunar parallax. A total lunar eclipse, in which the moon is
completely immersed in the earth's shadow, must take place at a
full moon if
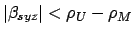 (see Fig. 28),
or equivalently
(see Fig. 28),
or equivalently
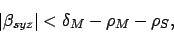 |
(145) |
and either a total or a partial lunar eclipse, in which the moon is only
partially immersed in the earth's shadow, must take place if
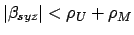 (see Fig. 28),
or equivalently
(see Fig. 28),
or equivalently
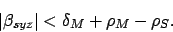 |
(146) |
Note that lunar eclipses are simultaneously
visible at all observation sites on the earth for which the moon is
above the horizon, since the earth's shadow is larger than the moon, and the relative position of the moon and the earth's shadow is not affected by parallax
(since both the moon and the shadow are the same distance from the earth).
The criterion for a solar eclipse is modified by lunar parallax, which causes the angular position of the moon relative to the sun to shift by up to 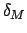 from its geocentric position. The amount of the shift
depends on the observation site. However, a site can always be found
at which the shift takes its maximum value in any particular direction.
Note that the sun has negligible parallax, since it is much further from the earth than the moon. Taking parallactic shifts into account, a total solar eclipse, in which the sun is totally obscured by the moon,
must take place if
from its geocentric position. The amount of the shift
depends on the observation site. However, a site can always be found
at which the shift takes its maximum value in any particular direction.
Note that the sun has negligible parallax, since it is much further from the earth than the moon. Taking parallactic shifts into account, a total solar eclipse, in which the sun is totally obscured by the moon,
must take place if  and
and
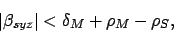 |
(147) |
an annular solar eclipse, in which all of the sun apart from
a thin outer ring is obscured by the moon, must take place if
 and
and
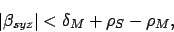 |
(148) |
and either a total, an annular, or a partial solar eclipse, in which the
sun is only partially obscured by the moon, must take place if
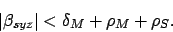 |
(149) |
As a consequence of lunar parallax, and the fact that the angular sizes of the sun and moon in the sky are very similar, solar eclipses are only visible in very localized regions of the earth. Note, finally, that the above criteria represent
necessary, but not sufficient, conditions for the occurrence of the various eclipses with which
they are associated. This is the case because the point of closest
approach of the moon and the earth's shadow, in the case of a
lunar eclipse, and the moon and sun, in the case of a solar eclipse, does
not necessarily occur exactly at the syzygy, due to the inclination
of the moon's orbit to the ecliptic. However, since the said inclination
is fairly gentle, the above criteria turn out to be very accurate
predictors of eclipses.
The criterion for a total lunar eclipse can be written
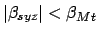 , where
, where
 |
(150) |
Here, the functions
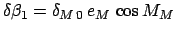 ,
,
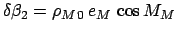 , and
, and
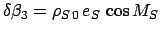 are tabulated in Table 43. The criterion for any type of
lunar eclipse becomes
are tabulated in Table 43. The criterion for any type of
lunar eclipse becomes
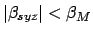 , where
, where
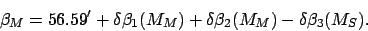 |
(151) |
The criterion for a total solar eclipse can
be written
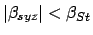 and
and
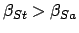 , where
, where
 |
(152) |
and
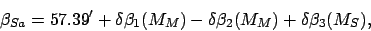 |
(153) |
The criterion for an annular solar eclipse is
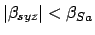 and
and
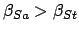 .
Finally,
the criterion for any
type of solar eclipse is
.
Finally,
the criterion for any
type of solar eclipse is
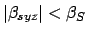 , where
, where
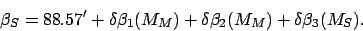 |
(154) |



Next: Example Eclipse Calculations
Up: Lunar-Solar Syzygies and Eclipses
Previous: Example Syzygy Calculations
Richard Fitzpatrick
2010-07-21
![]() , where
, where
![]() is the solar radius, and
is the solar radius, and ![]() the earth-sun distance. However,
the earth-sun distance. However,
![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are the major radius, eccentricity, and mean anomaly of the sun's apparent
orbit around the earth, respectively (see Cha. 4). Hence,
are the major radius, eccentricity, and mean anomaly of the sun's apparent
orbit around the earth, respectively (see Cha. 4). Hence,
![]() . Of course, once
the date and time of a syzygy has been established,
. Of course, once
the date and time of a syzygy has been established, ![]() can be calculated from Table 38. However, the lunar argument of latitude,
can be calculated from Table 38. However, the lunar argument of latitude, ![]() , must first be determined using
, must first be determined using
![]() (see Fig. 28),
or equivalently
(see Fig. 28),
or equivalently
![]() from its geocentric position. The amount of the shift
depends on the observation site. However, a site can always be found
at which the shift takes its maximum value in any particular direction.
Note that the sun has negligible parallax, since it is much further from the earth than the moon. Taking parallactic shifts into account, a total solar eclipse, in which the sun is totally obscured by the moon,
must take place if
from its geocentric position. The amount of the shift
depends on the observation site. However, a site can always be found
at which the shift takes its maximum value in any particular direction.
Note that the sun has negligible parallax, since it is much further from the earth than the moon. Taking parallactic shifts into account, a total solar eclipse, in which the sun is totally obscured by the moon,
must take place if ![]() and
and
![]() , where
, where