


Next: The Maxwell distribution
Up: Applications of statistical thermodynamics
Previous: Specific heats of gases
Specific heats of solids
Consider a simple solid containing  atoms. Now, atoms in solids cannot
translate (unlike those in gases), but
are free to vibrate about their equilibrium positions.
Such vibrations are called lattice vibrations, and can be thought of
as sound waves propagating
through the crystal lattice. Each atom is specified by three independent position
coordinates, and three conjugate momentum coordinates. Let us
only consider small amplitude vibrations.
In this case, we can expand the potential energy of interaction between the atoms
to give an expression which is quadratic in the atomic displacements
from their equilibrium positions. It is always possible to perform a
normal mode analysis
of the oscillations. In effect, we can find
atoms. Now, atoms in solids cannot
translate (unlike those in gases), but
are free to vibrate about their equilibrium positions.
Such vibrations are called lattice vibrations, and can be thought of
as sound waves propagating
through the crystal lattice. Each atom is specified by three independent position
coordinates, and three conjugate momentum coordinates. Let us
only consider small amplitude vibrations.
In this case, we can expand the potential energy of interaction between the atoms
to give an expression which is quadratic in the atomic displacements
from their equilibrium positions. It is always possible to perform a
normal mode analysis
of the oscillations. In effect, we can find 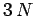 independent modes of oscillation of the solid.
Each mode has its own particular oscillation frequency, and its own particular pattern
of atomic displacements.
Any general oscillation can be written as a linear combination of these
normal modes.
Let
independent modes of oscillation of the solid.
Each mode has its own particular oscillation frequency, and its own particular pattern
of atomic displacements.
Any general oscillation can be written as a linear combination of these
normal modes.
Let 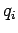 be the (appropriately normalized) amplitude of the
be the (appropriately normalized) amplitude of the 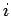 th normal mode,
and
th normal mode,
and 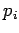 the momentum conjugate to this
coordinate. In normal mode coordinates, the total energy of the lattice vibrations takes the
particularly simple form
the momentum conjugate to this
coordinate. In normal mode coordinates, the total energy of the lattice vibrations takes the
particularly simple form
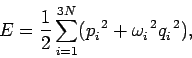 |
(499) |
where 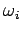 is the (angular) oscillation frequency of the
is the (angular) oscillation frequency of the 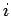 th normal mode. It is
clear that in normal mode coordinates, the linearized lattice vibrations are equivalent to
th normal mode. It is
clear that in normal mode coordinates, the linearized lattice vibrations are equivalent to
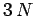 independent harmonic oscillators (of course, each oscillator corresponds to a different normal
mode).
independent harmonic oscillators (of course, each oscillator corresponds to a different normal
mode).
The typical value of 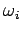 is the (angular) frequency of a sound wave
propagating through the lattice. Sound wave frequencies are far lower than the
typical vibration frequencies of gaseous molecules. In the latter case, the mass involved in the
vibration is simply that of the molecule, whereas in the former case the mass involved is that
of very many atoms (since lattice vibrations are non-localized). The strength of
interatomic bonds in gaseous molecules is similar to those in solids, so we can use the estimate
is the (angular) frequency of a sound wave
propagating through the lattice. Sound wave frequencies are far lower than the
typical vibration frequencies of gaseous molecules. In the latter case, the mass involved in the
vibration is simply that of the molecule, whereas in the former case the mass involved is that
of very many atoms (since lattice vibrations are non-localized). The strength of
interatomic bonds in gaseous molecules is similar to those in solids, so we can use the estimate
 (
( is the force constant which measures the strength of
interatomic bonds, and
is the force constant which measures the strength of
interatomic bonds, and  is the mass involved in the oscillation) as proof that the typical
frequencies of lattice vibrations are very
much less than the vibration frequencies of simple molecules.
It follows from
is the mass involved in the oscillation) as proof that the typical
frequencies of lattice vibrations are very
much less than the vibration frequencies of simple molecules.
It follows from
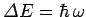 that the quantum energy levels of lattice vibrations are
far more closely spaced than the vibrational energy levels of gaseous molecules. Thus, it is
likely (and is, indeed, the case) that lattice vibrations are not frozen out at room temperature,
but, instead, make their full classical contribution to the molar specific heat of the solid.
that the quantum energy levels of lattice vibrations are
far more closely spaced than the vibrational energy levels of gaseous molecules. Thus, it is
likely (and is, indeed, the case) that lattice vibrations are not frozen out at room temperature,
but, instead, make their full classical contribution to the molar specific heat of the solid.
If the lattice vibrations behave classically then, according to the equipartition theorem,
each normal mode of oscillation has an associated mean energy 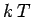 in equilibrium at
temperature
in equilibrium at
temperature  [
[ resides in the kinetic energy of the oscillation,
and
resides in the kinetic energy of the oscillation,
and  resides in the potential energy].
Thus, the mean internal energy per mole of the solid is
resides in the potential energy].
Thus, the mean internal energy per mole of the solid is
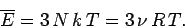 |
(500) |
It follows that the molar heat capacity at constant volume is
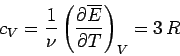 |
(501) |
for solids. This gives a value of 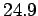 joules/mole/degree. In fact, at room temperature most
solids (in particular, metals)
have heat capacities which lie remarkably close to this value. This
fact was discovered
experimentally by Dulong and Petite at the beginning of the nineteenth century, and was used to
make some of the first
crude estimates of the molecular weights of solids (if we know the molar heat capacity
of a substance
then we can easily work out how much of it corresponds to one mole, and
by weighing this amount, and then dividing the result by Avogadro's number,
we can obtain an estimate of the molecular weight). Table 4 lists the experimental
molar heat
capacities
joules/mole/degree. In fact, at room temperature most
solids (in particular, metals)
have heat capacities which lie remarkably close to this value. This
fact was discovered
experimentally by Dulong and Petite at the beginning of the nineteenth century, and was used to
make some of the first
crude estimates of the molecular weights of solids (if we know the molar heat capacity
of a substance
then we can easily work out how much of it corresponds to one mole, and
by weighing this amount, and then dividing the result by Avogadro's number,
we can obtain an estimate of the molecular weight). Table 4 lists the experimental
molar heat
capacities 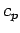 at constant pressure for various solids. The heat capacity at constant
volume is somewhat less than the constant pressure value, but not by much,
because solids
are fairly incompressible.
It can be seen that Dulong and Petite's law (i.e., that all solids have a molar heat capacities
close to
at constant pressure for various solids. The heat capacity at constant
volume is somewhat less than the constant pressure value, but not by much,
because solids
are fairly incompressible.
It can be seen that Dulong and Petite's law (i.e., that all solids have a molar heat capacities
close to 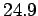 joules/mole/degree) holds pretty well for metals.
However, the law fails badly for
diamond. This is not surprising. As is well-known,
diamond is an extremely hard substance, so its intermolecular bonds must be very strong, suggesting
that the force constant
joules/mole/degree) holds pretty well for metals.
However, the law fails badly for
diamond. This is not surprising. As is well-known,
diamond is an extremely hard substance, so its intermolecular bonds must be very strong, suggesting
that the force constant  is large.
Diamond is also a fairly low density substance, so the mass
is large.
Diamond is also a fairly low density substance, so the mass  involved in
lattice vibrations is comparatively small. Both these facts suggest that the typical lattice vibration
frequency of diamond (
involved in
lattice vibrations is comparatively small. Both these facts suggest that the typical lattice vibration
frequency of diamond (
 ) is high. In fact, the spacing between
the different vibration energy
levels (which scales like
) is high. In fact, the spacing between
the different vibration energy
levels (which scales like
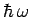 ) is sufficiently large in diamond for the vibrational
degrees of freedom
to be largely frozen out at room temperature. This accounts for the anomalously low
heat capacity of diamond in Tab. 4.
) is sufficiently large in diamond for the vibrational
degrees of freedom
to be largely frozen out at room temperature. This accounts for the anomalously low
heat capacity of diamond in Tab. 4.
Table 4:
Values of 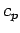 (joules/mole/degree) for some solids at
(joules/mole/degree) for some solids at  K. From Reif.
K. From Reif.
| Solid |
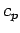 |
Solid |
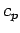 |
| Copper |
24.5 |
Aluminium |
24.4 |
| Silver |
25.5 |
Tin (white) |
26.4 |
| Lead |
26.4 |
Sulphur (rhombic) |
22.4 |
| Zinc |
25.4 |
Carbon (diamond) |
6.1 |
|
Dulong and Petite's law is essentially a high temperature limit. The molar heat capacity cannot
remain a constant as the temperature approaches absolute zero, since, by
Eq. (488), this
would imply
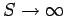 , which violates the third law of thermodynamics. We can make
a crude model of the behaviour of
, which violates the third law of thermodynamics. We can make
a crude model of the behaviour of 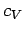 at low temperatures by assuming that all the normal
modes oscillate at the same frequency,
at low temperatures by assuming that all the normal
modes oscillate at the same frequency,  , say. This approximation was first employed by
Einstein in a paper published in 1907. According to Eq. (499),
the solid acts like a set
of
, say. This approximation was first employed by
Einstein in a paper published in 1907. According to Eq. (499),
the solid acts like a set
of 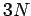 independent oscillators which, making use of
Einstein's approximation, all vibrate at the same frequency.
We can use the quantum mechanical result (479) for a single
oscillator to write the mean energy
of the solid in the form
independent oscillators which, making use of
Einstein's approximation, all vibrate at the same frequency.
We can use the quantum mechanical result (479) for a single
oscillator to write the mean energy
of the solid in the form
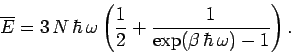 |
(502) |
The molar heat capacity is defined
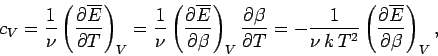 |
(503) |
giving
![\begin{displaymath}
c_V = - \frac{3 \,N_A \,\hbar \,\omega}{k\, T^2} \left[
-\fr...
...\hbar\, \omega}
{[\exp(\beta\,\hbar\, \omega) - 1]^2} \right],
\end{displaymath}](img1189.png) |
(504) |
which reduces to
![\begin{displaymath}
c_V = 3\,R \left(\frac{\theta_E}{T}\right)^2 \frac{\exp(\theta_E / T)}
{[\exp(\theta_E/T) - 1]^2}.
\end{displaymath}](img1190.png) |
(505) |
Here,
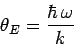 |
(506) |
is called the Einstein temperature. If the temperature is sufficiently
high that
 then
then
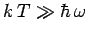 , and the above expression reduces to
, and the above expression reduces to
 , after expansion of the exponential functions. Thus, the law of Dulong and
Petite is recovered for temperatures significantly in excess of the Einstein temperature.
On the other hand, if the temperature is sufficiently
low that
, after expansion of the exponential functions. Thus, the law of Dulong and
Petite is recovered for temperatures significantly in excess of the Einstein temperature.
On the other hand, if the temperature is sufficiently
low that  then the
exponential factors in Eq. (505) become very much larger than unity, giving
then the
exponential factors in Eq. (505) become very much larger than unity, giving
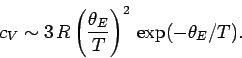 |
(507) |
So, in this simple model the specific heat approaches zero exponentially as
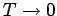 .
.
In reality, the specific heats of solids do not approach zero quite as quickly as
suggested by Einstein's model when
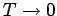 . The experimentally observed low temperature
behaviour is more like
. The experimentally observed low temperature
behaviour is more like
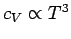 (see Fig. 6). The reason for this discrepancy is the crude
approximation
that all normal modes have the same frequency. In fact, long wavelength modes have lower frequencies
than short wavelength modes, so the former are much harder to freeze out than the latter
(because the spacing between quantum energy levels,
(see Fig. 6). The reason for this discrepancy is the crude
approximation
that all normal modes have the same frequency. In fact, long wavelength modes have lower frequencies
than short wavelength modes, so the former are much harder to freeze out than the latter
(because the spacing between quantum energy levels, 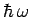 , is smaller in the former case).
The molar
heat capacity does not decrease with temperature as rapidly as suggested by Einstein's model
because these long wavelength modes are able to make a significant contribution
to the heat capacity even at very low
temperatures. A more realistic model of lattice vibrations was developed by the Dutch physicist
Peter Debye in 1912.
In the Debye model, the frequencies of the normal modes of vibration are estimated by treating
the solid as an isotropic continuous medium. This approach is reasonable because the only modes
which really matter at low temperatures are the long wavelength modes: i.e., those whose
wavelengths greatly exceed the interatomic spacing. It is plausible that these modes are not
particularly
sensitive to the discrete nature of the solid: i.e., the fact that it is made up of atoms
rather than being continuous.
, is smaller in the former case).
The molar
heat capacity does not decrease with temperature as rapidly as suggested by Einstein's model
because these long wavelength modes are able to make a significant contribution
to the heat capacity even at very low
temperatures. A more realistic model of lattice vibrations was developed by the Dutch physicist
Peter Debye in 1912.
In the Debye model, the frequencies of the normal modes of vibration are estimated by treating
the solid as an isotropic continuous medium. This approach is reasonable because the only modes
which really matter at low temperatures are the long wavelength modes: i.e., those whose
wavelengths greatly exceed the interatomic spacing. It is plausible that these modes are not
particularly
sensitive to the discrete nature of the solid: i.e., the fact that it is made up of atoms
rather than being continuous.
Consider a sound wave propagating through an isotropic continuous medium.
The disturbance varies with position vector 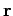 and time
and time  like
like
![$\exp[-{\rm i}\,({\bf k}\!\cdot{\bf r} - \omega \,t)]$](img1198.png) , where the wave-vector
, where the wave-vector  and
the frequency of oscillation
and
the frequency of oscillation  satisfy the dispersion relation for sound waves in
an isotropic medium:
satisfy the dispersion relation for sound waves in
an isotropic medium:
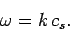 |
(508) |
Here,  is the speed of sound in the medium. Suppose, for the sake
of argument, that the medium is periodic in
the
is the speed of sound in the medium. Suppose, for the sake
of argument, that the medium is periodic in
the 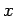 -,
-, 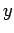 -, and
-, and 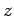 -directions with periodicity lengths
-directions with periodicity lengths 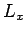 ,
,  , and
, and 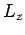 , respectively.
In order to maintain periodicity we need
, respectively.
In order to maintain periodicity we need
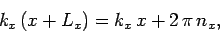 |
(509) |
where 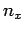 is an integer. There are analogous constraints on
is an integer. There are analogous constraints on 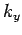 and
and 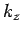 . It follows that
in a periodic medium the components of the wave-vector are quantized, and can only take the
values
. It follows that
in a periodic medium the components of the wave-vector are quantized, and can only take the
values
where  ,
,  , and
, and 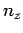 are all integers. It is assumed that
are all integers. It is assumed that 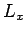 ,
,  , and
, and 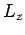 are
macroscopic lengths, so the allowed values of the components of the wave-vector are very closely
spaced.
For given values of
are
macroscopic lengths, so the allowed values of the components of the wave-vector are very closely
spaced.
For given values of 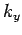 and
and 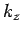 , the number of
allowed values of
, the number of
allowed values of 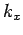 which lie in the range
which lie in the range 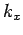 to
to 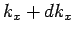 is given by
is given by
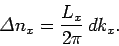 |
(513) |
It follows that the number of allowed values of  (i.e., the number of allowed
modes) when
(i.e., the number of allowed
modes) when 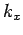 lies in the range
lies in the range 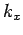 to
to 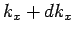 ,
,
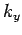 lies in the range
lies in the range 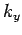 to
to 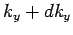 , and
, and
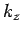 lies in the range
lies in the range 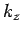 to
to 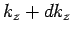 , is
, is
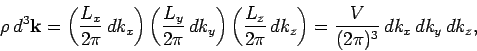 |
(514) |
where
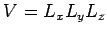 is the periodicity volume, and
is the periodicity volume, and
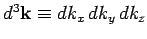 . The quantity
. The quantity 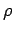 is called the density of modes.
Note that this density is independent of
is called the density of modes.
Note that this density is independent of  , and proportional to the periodicity
volume. Thus, the density of modes per unit volume is a constant independent of the magnitude
or shape of the periodicity
volume. The density of modes per unit volume when the magnitude of
, and proportional to the periodicity
volume. Thus, the density of modes per unit volume is a constant independent of the magnitude
or shape of the periodicity
volume. The density of modes per unit volume when the magnitude of  lies in
the range
lies in
the range 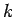 to
to  is given by multiplying the density of modes per unit volume by
the ``volume'' in
is given by multiplying the density of modes per unit volume by
the ``volume'' in  -space of the spherical shell lying between radii
-space of the spherical shell lying between radii 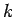 and
and  .
Thus,
.
Thus,
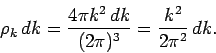 |
(515) |
Consider an isotropic continuous medium of volume 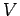 . According to the above
relation, the
number of normal modes whose frequencies lie between
. According to the above
relation, the
number of normal modes whose frequencies lie between  and
and
 (which is equivalent to the number of modes whose
(which is equivalent to the number of modes whose 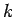 values lie in the range
values lie in the range 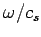 to
to
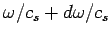 ) is
) is
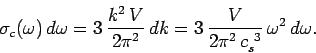 |
(516) |
The factor of 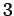 comes from the three possible polarizations of sound waves in solids.
For every allowed wavenumber (or frequency) there are two independent torsional modes,
where the displacement is perpendicular to the direction of propagation, and one
longitudinal mode, where the displacement is parallel to the direction of propagation.
Torsion waves are vaguely analogous to electromagnetic waves (these also have two
independent polarizations). The longitudinal mode is very similar to the compressional
sound wave in gases. Of course, torsion waves can not propagate in gases because gases
have no resistance to deformation without change of volume.
comes from the three possible polarizations of sound waves in solids.
For every allowed wavenumber (or frequency) there are two independent torsional modes,
where the displacement is perpendicular to the direction of propagation, and one
longitudinal mode, where the displacement is parallel to the direction of propagation.
Torsion waves are vaguely analogous to electromagnetic waves (these also have two
independent polarizations). The longitudinal mode is very similar to the compressional
sound wave in gases. Of course, torsion waves can not propagate in gases because gases
have no resistance to deformation without change of volume.
The Debye approach consists in approximating the actual density of normal modes
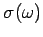 by the density in a continuous medium
by the density in a continuous medium
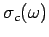 , not
only at low frequencies (long wavelengths) where these should be nearly the same, but
also at higher frequencies where they may differ substantially. Suppose that we are
dealing with a solid consisting of
, not
only at low frequencies (long wavelengths) where these should be nearly the same, but
also at higher frequencies where they may differ substantially. Suppose that we are
dealing with a solid consisting of  atoms. We know that there are
only
atoms. We know that there are
only 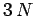 independent normal modes. It follows that we must cut off the
density of states above some critical frequency,
independent normal modes. It follows that we must cut off the
density of states above some critical frequency, 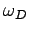 say, otherwise we
will have too many modes. Thus, in the Debye approximation the density
of normal modes takes the form
say, otherwise we
will have too many modes. Thus, in the Debye approximation the density
of normal modes takes the form
Here, 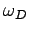 is the Debye frequency. This critical frequency is chosen such that
the total number of normal modes is
is the Debye frequency. This critical frequency is chosen such that
the total number of normal modes is 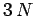 , so
, so
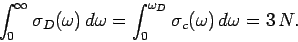 |
(518) |
Substituting Eq. (516) into the previous formula yields
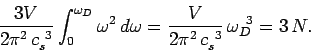 |
(519) |
This implies that
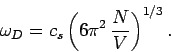 |
(520) |
Thus, the Debye frequency depends only on the sound velocity in the solid and the number
of atoms per unit volume. The wavelength corresponding to the Debye frequency
is
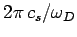 , which is clearly on the order of the interatomic spacing
, which is clearly on the order of the interatomic spacing
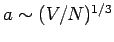 .
It follows that the cut-off of normal modes whose frequencies exceed the Debye frequency
is equivalent to a cut-off of normal modes whose wavelengths are less than the interatomic
spacing. Of course, it makes physical sense that such modes should be absent.
.
It follows that the cut-off of normal modes whose frequencies exceed the Debye frequency
is equivalent to a cut-off of normal modes whose wavelengths are less than the interatomic
spacing. Of course, it makes physical sense that such modes should be absent.
Figure 5:
The true density of normal modes in diamond compared with
the density of normal modes predicted by Debye theory. From C.B. Walker, Phys. Rev. 103, 547 (1956).
 |
Figure 5 compares the actual density of normal modes in diamond with
the density predicted by Debye theory.
Not surprisingly, there is not a particularly strong resemblance
between these two curves, since Debye theory is highly idealized.
Nevertheless, both curves exhibit sharp cut-offs at high frequencies, and
coincide at low frequencies. Furthermore, the areas under both curves are
the same. As we shall see,
this is sufficient to allow Debye theory to correctly account for
the temperature variation of the specific heat of solids at low temperatures.
We can use the quantum mechanical expression for the
mean energy of a single oscillator, Eq. (479), to calculate the mean
energy of lattice vibrations in the Debye approximation. We obtain
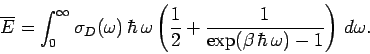 |
(521) |
According to Eq. (503), the molar heat capacity takes the form
![\begin{displaymath}
c_V = \frac{1}{\nu\, k\, T^2} \int_0^\infty \sigma_D (\omega...
...r\,\omega}
{[\exp(\beta\,\hbar\,\omega)-1]^2}\right]\,d\omega.
\end{displaymath}](img1247.png) |
(522) |
Substituting in Eq. (517), we find that
![\begin{displaymath}
c_V = \frac{k}{\nu}\int_0^{\omega_D} \frac{\exp(\beta\,\hbar...
...a)-1]^2}\,
\frac{3 \,V}{2\pi^2 \,c_s^{~3}}\,\omega^2\,d\omega,
\end{displaymath}](img1248.png) |
(523) |
giving
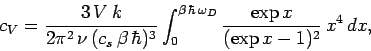 |
(524) |
in terms of the dimensionless variable
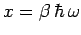 .
According to Eq. (520), the volume can be written
.
According to Eq. (520), the volume can be written
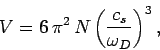 |
(525) |
so the heat capacity reduces to
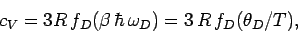 |
(526) |
where the Debye function is defined
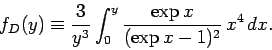 |
(527) |
We have also defined the Debye temperature 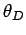 as
as
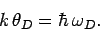 |
(528) |
Consider the asymptotic limit in which 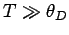 . For small
. For small 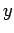 , we can approximate
, we can approximate
 as
as 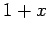 in the integrand of Eq. (527), so that
in the integrand of Eq. (527), so that
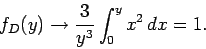 |
(529) |
Thus, if the temperature greatly exceeds the Debye temperature we recover the law of
Dulong and Petite that  . Consider, now, the
asymptotic limit in which
. Consider, now, the
asymptotic limit in which 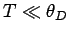 . For large
. For large 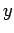 ,
,
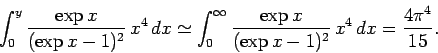 |
(530) |
The latter integration is standard (if rather obscure), and can be looked up in any
(large) reference book
on integration. Thus, in the low temperature limit
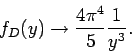 |
(531) |
This yields
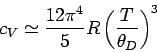 |
(532) |
in the limit 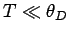 : i.e.,
: i.e., 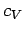 varies with temperature like
varies with temperature like 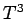 .
.
Table 5:
Comparison of Debye temperatures (in degrees kelvin) obtained from the
low temperature behaviour of the heat capacity with those calculated from the
sound speed. From C. Kittel, Introduction to solid-state physics, 2nd Ed. (John Wiley & Sons, New York NY, 1956).
| Solid |
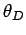 from low temp. from low temp. |
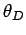 from sound speed from sound speed |
| NaCl |
308 |
320 |
| KCl |
230 |
246 |
| Ag |
225 |
216 |
| Zn |
308 |
305 |
|
The fact that 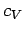 goes like
goes like 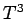 at low temperatures is quite well verified experimentally,
although it is sometimes necessary to go to temperatures as low as
at low temperatures is quite well verified experimentally,
although it is sometimes necessary to go to temperatures as low as
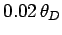 to obtain
this asymptotic behaviour. Theoretically,
to obtain
this asymptotic behaviour. Theoretically, 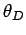 should be calculable from
Eq. (520)
in terms of the sound speed in the solid and the molar volume. Table 5 shows a
comparison of Debye temperatures evaluated by this means with temperatures obtained
empirically by fitting the law (532) to the low temperature variation of the
heat capacity. It can be seen that there is fairly good agreement between the theoretical and
empirical Debye temperatures. This suggests that the Debye theory affords a good, thought not
perfect, representation of the behaviour of
should be calculable from
Eq. (520)
in terms of the sound speed in the solid and the molar volume. Table 5 shows a
comparison of Debye temperatures evaluated by this means with temperatures obtained
empirically by fitting the law (532) to the low temperature variation of the
heat capacity. It can be seen that there is fairly good agreement between the theoretical and
empirical Debye temperatures. This suggests that the Debye theory affords a good, thought not
perfect, representation of the behaviour of 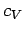 in solids over the entire temperature range.
in solids over the entire temperature range.
Figure 6:
The molar heat capacity of various solids.
 |
Finally, Fig. 6 shows the actual temperature variation of the molar heat capacities
of various solids as well as that predicted by Debye's theory. The prediction of Einstein's theory
is also show for the sake of comparison. Note that 24.9 joules/mole/degree is about
6 calories/gram-atom/degree (the latter are chemist's units).



Next: The Maxwell distribution
Up: Applications of statistical thermodynamics
Previous: Specific heats of gases
Richard Fitzpatrick
2006-02-02
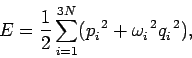
![]() is the (angular) frequency of a sound wave
propagating through the lattice. Sound wave frequencies are far lower than the
typical vibration frequencies of gaseous molecules. In the latter case, the mass involved in the
vibration is simply that of the molecule, whereas in the former case the mass involved is that
of very many atoms (since lattice vibrations are non-localized). The strength of
interatomic bonds in gaseous molecules is similar to those in solids, so we can use the estimate
is the (angular) frequency of a sound wave
propagating through the lattice. Sound wave frequencies are far lower than the
typical vibration frequencies of gaseous molecules. In the latter case, the mass involved in the
vibration is simply that of the molecule, whereas in the former case the mass involved is that
of very many atoms (since lattice vibrations are non-localized). The strength of
interatomic bonds in gaseous molecules is similar to those in solids, so we can use the estimate
 (
(![]() is the force constant which measures the strength of
interatomic bonds, and
is the force constant which measures the strength of
interatomic bonds, and ![]() is the mass involved in the oscillation) as proof that the typical
frequencies of lattice vibrations are very
much less than the vibration frequencies of simple molecules.
It follows from
is the mass involved in the oscillation) as proof that the typical
frequencies of lattice vibrations are very
much less than the vibration frequencies of simple molecules.
It follows from
![]() that the quantum energy levels of lattice vibrations are
far more closely spaced than the vibrational energy levels of gaseous molecules. Thus, it is
likely (and is, indeed, the case) that lattice vibrations are not frozen out at room temperature,
but, instead, make their full classical contribution to the molar specific heat of the solid.
that the quantum energy levels of lattice vibrations are
far more closely spaced than the vibrational energy levels of gaseous molecules. Thus, it is
likely (and is, indeed, the case) that lattice vibrations are not frozen out at room temperature,
but, instead, make their full classical contribution to the molar specific heat of the solid.
![]() in equilibrium at
temperature
in equilibrium at
temperature ![]() [
[![]() resides in the kinetic energy of the oscillation,
and
resides in the kinetic energy of the oscillation,
and ![]() resides in the potential energy].
Thus, the mean internal energy per mole of the solid is
resides in the potential energy].
Thus, the mean internal energy per mole of the solid is
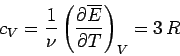
 ) is high. In fact, the spacing between
the different vibration energy
levels (which scales like
) is high. In fact, the spacing between
the different vibration energy
levels (which scales like
![]() , which violates the third law of thermodynamics. We can make
a crude model of the behaviour of
, which violates the third law of thermodynamics. We can make
a crude model of the behaviour of ![]() at low temperatures by assuming that all the normal
modes oscillate at the same frequency,
at low temperatures by assuming that all the normal
modes oscillate at the same frequency, ![]() , say. This approximation was first employed by
Einstein in a paper published in 1907. According to Eq. (499),
the solid acts like a set
of
, say. This approximation was first employed by
Einstein in a paper published in 1907. According to Eq. (499),
the solid acts like a set
of ![]() independent oscillators which, making use of
Einstein's approximation, all vibrate at the same frequency.
We can use the quantum mechanical result (479) for a single
oscillator to write the mean energy
of the solid in the form
independent oscillators which, making use of
Einstein's approximation, all vibrate at the same frequency.
We can use the quantum mechanical result (479) for a single
oscillator to write the mean energy
of the solid in the form
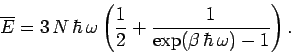
![\begin{displaymath}
c_V = - \frac{3 \,N_A \,\hbar \,\omega}{k\, T^2} \left[
-\fr...
...\hbar\, \omega}
{[\exp(\beta\,\hbar\, \omega) - 1]^2} \right],
\end{displaymath}](img1189.png)
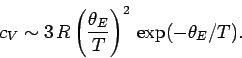
![]() . The experimentally observed low temperature
behaviour is more like
. The experimentally observed low temperature
behaviour is more like
![]() (see Fig. 6). The reason for this discrepancy is the crude
approximation
that all normal modes have the same frequency. In fact, long wavelength modes have lower frequencies
than short wavelength modes, so the former are much harder to freeze out than the latter
(because the spacing between quantum energy levels,
(see Fig. 6). The reason for this discrepancy is the crude
approximation
that all normal modes have the same frequency. In fact, long wavelength modes have lower frequencies
than short wavelength modes, so the former are much harder to freeze out than the latter
(because the spacing between quantum energy levels, ![]() , is smaller in the former case).
The molar
heat capacity does not decrease with temperature as rapidly as suggested by Einstein's model
because these long wavelength modes are able to make a significant contribution
to the heat capacity even at very low
temperatures. A more realistic model of lattice vibrations was developed by the Dutch physicist
Peter Debye in 1912.
In the Debye model, the frequencies of the normal modes of vibration are estimated by treating
the solid as an isotropic continuous medium. This approach is reasonable because the only modes
which really matter at low temperatures are the long wavelength modes: i.e., those whose
wavelengths greatly exceed the interatomic spacing. It is plausible that these modes are not
particularly
sensitive to the discrete nature of the solid: i.e., the fact that it is made up of atoms
rather than being continuous.
, is smaller in the former case).
The molar
heat capacity does not decrease with temperature as rapidly as suggested by Einstein's model
because these long wavelength modes are able to make a significant contribution
to the heat capacity even at very low
temperatures. A more realistic model of lattice vibrations was developed by the Dutch physicist
Peter Debye in 1912.
In the Debye model, the frequencies of the normal modes of vibration are estimated by treating
the solid as an isotropic continuous medium. This approach is reasonable because the only modes
which really matter at low temperatures are the long wavelength modes: i.e., those whose
wavelengths greatly exceed the interatomic spacing. It is plausible that these modes are not
particularly
sensitive to the discrete nature of the solid: i.e., the fact that it is made up of atoms
rather than being continuous.
![]() and time
and time ![]() like
like
![]() , where the wave-vector
, where the wave-vector ![]() and
the frequency of oscillation
and
the frequency of oscillation ![]() satisfy the dispersion relation for sound waves in
an isotropic medium:
satisfy the dispersion relation for sound waves in
an isotropic medium:
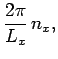
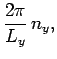

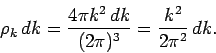
![]() . According to the above
relation, the
number of normal modes whose frequencies lie between
. According to the above
relation, the
number of normal modes whose frequencies lie between ![]() and
and
![]() (which is equivalent to the number of modes whose
(which is equivalent to the number of modes whose ![]() values lie in the range
values lie in the range ![]() to
to
![]() ) is
) is
![]() by the density in a continuous medium
by the density in a continuous medium
![]() , not
only at low frequencies (long wavelengths) where these should be nearly the same, but
also at higher frequencies where they may differ substantially. Suppose that we are
dealing with a solid consisting of
, not
only at low frequencies (long wavelengths) where these should be nearly the same, but
also at higher frequencies where they may differ substantially. Suppose that we are
dealing with a solid consisting of ![]() atoms. We know that there are
only
atoms. We know that there are
only ![]() independent normal modes. It follows that we must cut off the
density of states above some critical frequency,
independent normal modes. It follows that we must cut off the
density of states above some critical frequency, ![]() say, otherwise we
will have too many modes. Thus, in the Debye approximation the density
of normal modes takes the form
say, otherwise we
will have too many modes. Thus, in the Debye approximation the density
of normal modes takes the form
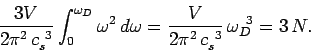

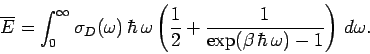
![\begin{displaymath}
c_V = \frac{1}{\nu\, k\, T^2} \int_0^\infty \sigma_D (\omega...
...r\,\omega}
{[\exp(\beta\,\hbar\,\omega)-1]^2}\right]\,d\omega.
\end{displaymath}](img1247.png)
![\begin{displaymath}
c_V = \frac{k}{\nu}\int_0^{\omega_D} \frac{\exp(\beta\,\hbar...
...a)-1]^2}\,
\frac{3 \,V}{2\pi^2 \,c_s^{~3}}\,\omega^2\,d\omega,
\end{displaymath}](img1248.png)
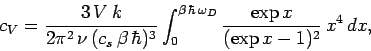
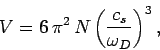
![]() . For small
. For small ![]() , we can approximate
, we can approximate
![]() as
as ![]() in the integrand of Eq. (527), so that
in the integrand of Eq. (527), so that
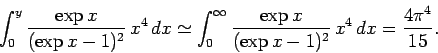
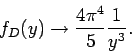
![]() goes like
goes like ![]() at low temperatures is quite well verified experimentally,
although it is sometimes necessary to go to temperatures as low as
at low temperatures is quite well verified experimentally,
although it is sometimes necessary to go to temperatures as low as
![]() to obtain
this asymptotic behaviour. Theoretically,
to obtain
this asymptotic behaviour. Theoretically, ![]() should be calculable from
Eq. (520)
in terms of the sound speed in the solid and the molar volume. Table 5 shows a
comparison of Debye temperatures evaluated by this means with temperatures obtained
empirically by fitting the law (532) to the low temperature variation of the
heat capacity. It can be seen that there is fairly good agreement between the theoretical and
empirical Debye temperatures. This suggests that the Debye theory affords a good, thought not
perfect, representation of the behaviour of
should be calculable from
Eq. (520)
in terms of the sound speed in the solid and the molar volume. Table 5 shows a
comparison of Debye temperatures evaluated by this means with temperatures obtained
empirically by fitting the law (532) to the low temperature variation of the
heat capacity. It can be seen that there is fairly good agreement between the theoretical and
empirical Debye temperatures. This suggests that the Debye theory affords a good, thought not
perfect, representation of the behaviour of ![]() in solids over the entire temperature range.
in solids over the entire temperature range.