


Next: Specific heats
Up: Applications of statistical thermodynamics
Previous: The equipartition theorem
Harmonic oscillators
Our proof of the equipartition theorem depends crucially on the classical approximation. To see how
quantum effects modify this result, let us examine a particularly simple system
which we know how to analyze using both classical and quantum physics: i.e.,
a
simple harmonic oscillator. Consider a one-dimensional harmonic oscillator in equilibrium
with a heat reservoir at temperature  . The energy of the oscillator is given by
. The energy of the oscillator is given by
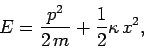 |
(467) |
where the first term on the right-hand side is the kinetic energy, involving the momentum
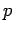 and mass
and mass  , and the second term is the potential energy, involving the displacement
, and the second term is the potential energy, involving the displacement
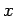 and the force constant
and the force constant  . Each of these terms is quadratic in the respective
variable. So, in the classical approximation the equipartition theorem yields:
. Each of these terms is quadratic in the respective
variable. So, in the classical approximation the equipartition theorem yields:
That is, the mean kinetic energy of the oscillator is equal
to the mean potential energy which
equals  . It follows that the mean total energy is
. It follows that the mean total energy is
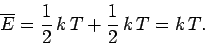 |
(470) |
According to quantum mechanics, the energy levels of a harmonic oscillator are equally
spaced and satisfy
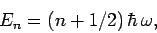 |
(471) |
where  is a non-negative integer, and
is a non-negative integer, and
 |
(472) |
The partition function for such an oscillator is given by
![\begin{displaymath}
Z = \sum_{n=0}^\infty \exp(-\beta \,E_n) = \exp[-(1/2)\,\bet...
... \,\omega]
\sum_{n=0}^\infty \exp(- n\,\beta\, \hbar\,\omega).
\end{displaymath}](img1092.png) |
(473) |
Now,
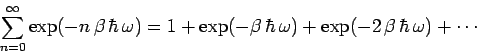 |
(474) |
is simply the sum of an infinite geometric series, and can be evaluated immediately,
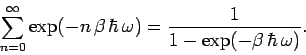 |
(475) |
Thus, the partition function takes the form
![\begin{displaymath}
Z = \frac{ \exp[-(1/2)\,\beta\,\hbar\,\omega]}{1-\exp(-\beta\,\hbar\,\omega)},
\end{displaymath}](img1095.png) |
(476) |
and
![\begin{displaymath}
\ln Z = - \frac{1}{2}\,\beta\,\hbar\,\omega -\ln [1- \exp(-\beta\,\hbar\,\omega)]
\end{displaymath}](img1096.png) |
(477) |
The mean energy of the oscillator is given by [see Eq. (399)]
![\begin{displaymath}
\overline{E} = - \frac{\partial}{\partial \beta} \ln Z = -
\...
...omega)\,\hbar\,\omega}
{1-\exp(-\beta\,\hbar\,\omega)}\right],
\end{displaymath}](img1097.png) |
(478) |
or
![\begin{displaymath}
\overline{E} = \hbar \,\omega \left[ \frac{1}{2} + \frac{1}{\exp(\beta\, \hbar\,
\omega)-1}
\right].
\end{displaymath}](img1098.png) |
(479) |
Consider the limit
 |
(480) |
in which the thermal energy 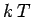 is large compared to the separation
is large compared to the separation
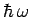 between the
energy levels. In this limit,
between the
energy levels. In this limit,
 |
(481) |
so
![\begin{displaymath}
\overline{E} \simeq \hbar\,\omega\left[\frac{1}{2} + \frac{1...
...meq \hbar\,\omega\left[ \frac{1}{\beta\,\hbar\,\omega}\right],
\end{displaymath}](img1102.png) |
(482) |
giving
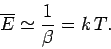 |
(483) |
Thus, the classical result (470) holds whenever the thermal energy greatly exceeds the typical
spacing between quantum energy levels.
Consider the limit
 |
(484) |
in which the thermal energy is small compared to the separation between
the energy levels. In this limit,
 |
(485) |
and so
![\begin{displaymath}
\overline{E} \simeq \hbar\,\omega \,[ 1/2 + \exp(-\beta\,\hbar\,\omega)] \simeq
\frac{1}{2} \,\hbar \,\omega.
\end{displaymath}](img1106.png) |
(486) |
Thus, if the thermal energy is much less than the spacing between quantum states then
the mean energy approaches that of the ground-state (the so-called zero point
energy).
Clearly, the equipartition theorem is only valid in the former limit, where
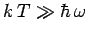 , and the oscillator possess sufficient thermal energy to explore many
of its possible quantum states.
, and the oscillator possess sufficient thermal energy to explore many
of its possible quantum states.



Next: Specific heats
Up: Applications of statistical thermodynamics
Previous: The equipartition theorem
Richard Fitzpatrick
2006-02-02

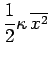
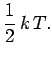
![\begin{displaymath}
Z = \sum_{n=0}^\infty \exp(-\beta \,E_n) = \exp[-(1/2)\,\bet...
... \,\omega]
\sum_{n=0}^\infty \exp(- n\,\beta\, \hbar\,\omega).
\end{displaymath}](img1092.png)
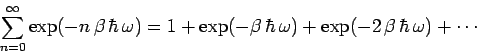
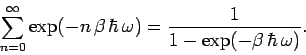
![\begin{displaymath}
Z = \frac{ \exp[-(1/2)\,\beta\,\hbar\,\omega]}{1-\exp(-\beta\,\hbar\,\omega)},
\end{displaymath}](img1095.png)
![\begin{displaymath}
\overline{E} = - \frac{\partial}{\partial \beta} \ln Z = -
\...
...omega)\,\hbar\,\omega}
{1-\exp(-\beta\,\hbar\,\omega)}\right],
\end{displaymath}](img1097.png)
![\begin{displaymath}
\overline{E} \simeq \hbar\,\omega\left[\frac{1}{2} + \frac{1...
...meq \hbar\,\omega\left[ \frac{1}{\beta\,\hbar\,\omega}\right],
\end{displaymath}](img1102.png)