


Next: Specific heats of gases
Up: Applications of statistical thermodynamics
Previous: Harmonic oscillators
We have discussed the internal energies and entropies of
substances (mostly ideal gases)
at some length. Unfortunately, these quantities cannot be directly
measured.
Instead, they must
be inferred from other information. The thermodynamic property of substances which
is the easiest to measure is, of course, the heat capacity, or specific heat. In fact,
once the variation of the specific heat with temperature is known, both the internal
energy and entropy can be easily reconstructed via
Here, use has been made of
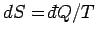 , and the third law of thermodynamics.
Clearly, the optimum way of verifying the results of statistical thermodynamics
is to compare the
theoretically predicted heat capacities with the experimentally measured values.
, and the third law of thermodynamics.
Clearly, the optimum way of verifying the results of statistical thermodynamics
is to compare the
theoretically predicted heat capacities with the experimentally measured values.
Classical physics, in the guise of the equipartition theorem, says that each
independent degree of freedom associated with a quadratic term in the energy
possesses an average energy  in thermal equilibrium at temperature
in thermal equilibrium at temperature
 . Consider a substance made up of
. Consider a substance made up of  molecules. Every molecular
degree of freedom contributes
molecules. Every molecular
degree of freedom contributes
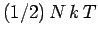 ,
or
,
or
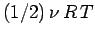 , to the mean energy of the substance (with the tacit proviso
that each degree of freedom is associated with a quadratic term in the energy).
Thus, the contribution to the molar heat capacity at constant volume (we wish to
avoid the complications associated with any external work done on the substance) is
, to the mean energy of the substance (with the tacit proviso
that each degree of freedom is associated with a quadratic term in the energy).
Thus, the contribution to the molar heat capacity at constant volume (we wish to
avoid the complications associated with any external work done on the substance) is
![\begin{displaymath}
\frac{1}{\nu}\left(
\frac{\partial \overline{E}}{\partial T}...
...{\partial[ (1/2)\, \nu\, R\,T] }{\partial T}= \frac{1}{2}\, R,
\end{displaymath}](img1114.png) |
(489) |
per molecular degree of freedom. The total classical heat capacity is
therefore
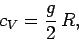 |
(490) |
where 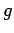 is the number of molecular degrees of freedom. Since large complicated
molecules clearly have very many more degrees of freedom than small simple
molecules, the above formula predicts that the molar
heat capacities of substances
made up of the former type of molecules
should greatly exceed those of substances made
up of the latter. In fact, the experimental heat capacities of substances containing
complicated molecules are generally greater than those of
substances containing simple molecules,
but by nowhere near the large factor predicted by Eq. (490). This equation also
implies that heat capacities are temperature independent. In fact,
this is not the case for most substances.
Experimental heat capacities generally increase with
increasing temperature. These two experimental
facts pose severe problems for classical physics.
Incidentally, these problems
were fully appreciated as far back as 1850. Stories that physicists at the end
of the nineteenth
century
thought that classical physics explained absolutely everything are largely apocryphal.
is the number of molecular degrees of freedom. Since large complicated
molecules clearly have very many more degrees of freedom than small simple
molecules, the above formula predicts that the molar
heat capacities of substances
made up of the former type of molecules
should greatly exceed those of substances made
up of the latter. In fact, the experimental heat capacities of substances containing
complicated molecules are generally greater than those of
substances containing simple molecules,
but by nowhere near the large factor predicted by Eq. (490). This equation also
implies that heat capacities are temperature independent. In fact,
this is not the case for most substances.
Experimental heat capacities generally increase with
increasing temperature. These two experimental
facts pose severe problems for classical physics.
Incidentally, these problems
were fully appreciated as far back as 1850. Stories that physicists at the end
of the nineteenth
century
thought that classical physics explained absolutely everything are largely apocryphal.
The equipartition theorem (and the whole classical approximation) is only valid
when the typical thermal energy 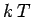 greatly exceeds the spacing between quantum
energy levels. Suppose that the temperature is sufficiently low that this
condition is not satisfied for one particular molecular degree of freedom.
In fact, suppose that
greatly exceeds the spacing between quantum
energy levels. Suppose that the temperature is sufficiently low that this
condition is not satisfied for one particular molecular degree of freedom.
In fact, suppose that 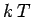 is much less than the spacing between
the energy levels.
According to Sect. 7.9, in this situation the degree of freedom only contributes
the ground-state energy,
is much less than the spacing between
the energy levels.
According to Sect. 7.9, in this situation the degree of freedom only contributes
the ground-state energy, 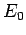 , say, to the mean energy of the molecule. The
ground-state energy can be a quite complicated
function of the internal properties of the
molecule, but is certainly not a function of the temperature, since this is
a collective property of all molecules. It follows that the contribution to
the molar heat capacity is
, say, to the mean energy of the molecule. The
ground-state energy can be a quite complicated
function of the internal properties of the
molecule, but is certainly not a function of the temperature, since this is
a collective property of all molecules. It follows that the contribution to
the molar heat capacity is
![\begin{displaymath}
\frac{1}{\nu}\left(
\frac{\partial [N E_0]}{\partial T}\right)_V = 0.
\end{displaymath}](img1116.png) |
(491) |
Thus, if 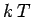 is much less than the spacing between the energy levels then
the degree of
freedom contributes nothing at all
to the molar heat capacity. We say that this particular
degree of freedom is frozen out. Clearly, at very low temperatures just about
all degrees of freedom are frozen out. As the temperature is gradually increased,
degrees of freedom successively
``kick in,'' and eventually contribute their full
is much less than the spacing between the energy levels then
the degree of
freedom contributes nothing at all
to the molar heat capacity. We say that this particular
degree of freedom is frozen out. Clearly, at very low temperatures just about
all degrees of freedom are frozen out. As the temperature is gradually increased,
degrees of freedom successively
``kick in,'' and eventually contribute their full 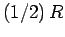 to
the molar heat capacity, as
to
the molar heat capacity, as 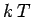 approaches, and then greatly exceeds, the spacing
between their
quantum energy levels. We can use these simple ideas to explain the behaviours
of most
experimental heat capacities.
approaches, and then greatly exceeds, the spacing
between their
quantum energy levels. We can use these simple ideas to explain the behaviours
of most
experimental heat capacities.
To make further progress, we need to
estimate the typical spacing between the quantum energy levels
associated with various degrees of freedom.
We can do this by observing the
frequency
of the electromagnetic radiation emitted and absorbed during transitions between
these energy levels. If the typical spacing between energy levels is
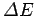 then
transitions between the various levels are associated with photons of
frequency
then
transitions between the various levels are associated with photons of
frequency 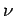 , where
, where
 . We can define an effective
temperature of the radiation via
. We can define an effective
temperature of the radiation via
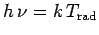 . If
. If
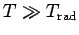 then
then
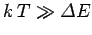 , and the degree of freedom makes its
full contribution to the heat capacity. On the other hand, if
, and the degree of freedom makes its
full contribution to the heat capacity. On the other hand, if
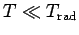 then
then
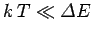 , and the degree of freedom is frozen out.
Table 3 lists the ``temperatures'' of various different types of radiation.
It is clear that degrees of freedom which give rise to emission or absorption
of radio or microwave radiation contribute their full
, and the degree of freedom is frozen out.
Table 3 lists the ``temperatures'' of various different types of radiation.
It is clear that degrees of freedom which give rise to emission or absorption
of radio or microwave radiation contribute their full 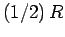 to the molar heat capacity at room temperature. Degrees of freedom which give rise to
emission or absorption in the visible, ultraviolet, X-ray, or
to the molar heat capacity at room temperature. Degrees of freedom which give rise to
emission or absorption in the visible, ultraviolet, X-ray, or 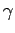 -ray
regions of the electromagnetic spectrum are frozen out at room temperature.
Degrees of freedom which emit or absorb infrared radiation are on the border line.
-ray
regions of the electromagnetic spectrum are frozen out at room temperature.
Degrees of freedom which emit or absorb infrared radiation are on the border line.
Table 3:
Effective ``temperatures'' of various types of electromagnetic radiation
| Radiation type |
Frequency (Hz) |
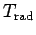 ( ( K) K) |
| Radio |
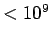 |
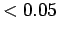 |
| Microwave |
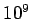 - - 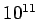 |
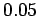 - - 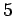 |
| Infrared |
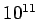 - -  |
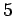 - - 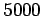 |
| Visible |
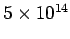 |
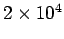 |
| Ultraviolet |
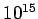 - -  |
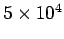 - -  |
| X-ray |
 - - 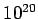 |
 - - 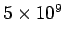 |
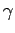 -ray -ray |
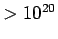 |
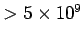 |
|



Next: Specific heats of gases
Up: Applications of statistical thermodynamics
Previous: Harmonic oscillators
Richard Fitzpatrick
2006-02-02


![]() in thermal equilibrium at temperature
in thermal equilibrium at temperature
![]() . Consider a substance made up of
. Consider a substance made up of ![]() molecules. Every molecular
degree of freedom contributes
molecules. Every molecular
degree of freedom contributes
![]() ,
or
,
or
![]() , to the mean energy of the substance (with the tacit proviso
that each degree of freedom is associated with a quadratic term in the energy).
Thus, the contribution to the molar heat capacity at constant volume (we wish to
avoid the complications associated with any external work done on the substance) is
, to the mean energy of the substance (with the tacit proviso
that each degree of freedom is associated with a quadratic term in the energy).
Thus, the contribution to the molar heat capacity at constant volume (we wish to
avoid the complications associated with any external work done on the substance) is
![\begin{displaymath}
\frac{1}{\nu}\left(
\frac{\partial \overline{E}}{\partial T}...
...{\partial[ (1/2)\, \nu\, R\,T] }{\partial T}= \frac{1}{2}\, R,
\end{displaymath}](img1114.png)
![]() greatly exceeds the spacing between quantum
energy levels. Suppose that the temperature is sufficiently low that this
condition is not satisfied for one particular molecular degree of freedom.
In fact, suppose that
greatly exceeds the spacing between quantum
energy levels. Suppose that the temperature is sufficiently low that this
condition is not satisfied for one particular molecular degree of freedom.
In fact, suppose that ![]() is much less than the spacing between
the energy levels.
According to Sect. 7.9, in this situation the degree of freedom only contributes
the ground-state energy,
is much less than the spacing between
the energy levels.
According to Sect. 7.9, in this situation the degree of freedom only contributes
the ground-state energy, ![]() , say, to the mean energy of the molecule. The
ground-state energy can be a quite complicated
function of the internal properties of the
molecule, but is certainly not a function of the temperature, since this is
a collective property of all molecules. It follows that the contribution to
the molar heat capacity is
, say, to the mean energy of the molecule. The
ground-state energy can be a quite complicated
function of the internal properties of the
molecule, but is certainly not a function of the temperature, since this is
a collective property of all molecules. It follows that the contribution to
the molar heat capacity is
![\begin{displaymath}
\frac{1}{\nu}\left(
\frac{\partial [N E_0]}{\partial T}\right)_V = 0.
\end{displaymath}](img1116.png)
![]() then
transitions between the various levels are associated with photons of
frequency
then
transitions between the various levels are associated with photons of
frequency ![]() , where
, where
![]() . We can define an effective
temperature of the radiation via
. We can define an effective
temperature of the radiation via
![]() . If
. If
![]() then
then
![]() , and the degree of freedom makes its
full contribution to the heat capacity. On the other hand, if
, and the degree of freedom makes its
full contribution to the heat capacity. On the other hand, if
![]() then
then
![]() , and the degree of freedom is frozen out.
Table 3 lists the ``temperatures'' of various different types of radiation.
It is clear that degrees of freedom which give rise to emission or absorption
of radio or microwave radiation contribute their full
, and the degree of freedom is frozen out.
Table 3 lists the ``temperatures'' of various different types of radiation.
It is clear that degrees of freedom which give rise to emission or absorption
of radio or microwave radiation contribute their full ![]() to the molar heat capacity at room temperature. Degrees of freedom which give rise to
emission or absorption in the visible, ultraviolet, X-ray, or
to the molar heat capacity at room temperature. Degrees of freedom which give rise to
emission or absorption in the visible, ultraviolet, X-ray, or ![]() -ray
regions of the electromagnetic spectrum are frozen out at room temperature.
Degrees of freedom which emit or absorb infrared radiation are on the border line.
-ray
regions of the electromagnetic spectrum are frozen out at room temperature.
Degrees of freedom which emit or absorb infrared radiation are on the border line.