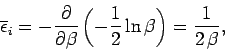Next: Harmonic oscillators
Up: Applications of statistical thermodynamics
Previous: Gibb's paradox
The equipartition theorem
The internal energy of a monatomic ideal gas containing  particles is
particles is
 .
This means that each particle possess, on average,
.
This means that each particle possess, on average,  units of energy.
Monatomic particles have only three translational degrees
of freedom, corresponding to
their motion in three dimensions. They possess no internal
rotational or vibrational degrees of freedom. Thus, the mean energy per degree of
freedom in a monatomic ideal gas is
units of energy.
Monatomic particles have only three translational degrees
of freedom, corresponding to
their motion in three dimensions. They possess no internal
rotational or vibrational degrees of freedom. Thus, the mean energy per degree of
freedom in a monatomic ideal gas is  . In fact,
this is a special case of a rather general result. Let us now try to prove this.
. In fact,
this is a special case of a rather general result. Let us now try to prove this.
Suppose that the energy of a
system is determined by some 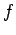 generalized coordinates
generalized coordinates 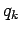 and corresponding
and corresponding 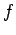 generalized momenta
generalized momenta  , so that
, so that
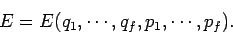 |
(455) |
Suppose further that:
- The total energy splits additively into the form
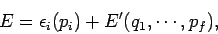 |
(456) |
where 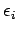 involves only one variable
involves only one variable 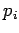 , and the remaining part
, and the remaining part
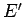 does not depend on
does not depend on 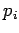 .
.
- The function
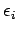 is quadratic in
is quadratic in 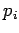 , so that
, so that
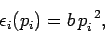 |
(457) |
where  is a constant.
is a constant.
The most common situation in which the above assumptions are valid is where
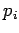 is a momentum. This is because the kinetic energy is usually a quadratic
function of each momentum component, whereas the potential energy does not
involve the momenta at all. However, if a coordinate
is a momentum. This is because the kinetic energy is usually a quadratic
function of each momentum component, whereas the potential energy does not
involve the momenta at all. However, if a coordinate 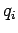 were to satisfy
assumptions 1 and 2 then the theorem we are about to establish would hold just
as well.
were to satisfy
assumptions 1 and 2 then the theorem we are about to establish would hold just
as well.
What is the mean value of 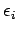 in thermal equilibrium if conditions
1 and 2 are satisfied? If the system is in equilibrium at absolute temperature
in thermal equilibrium if conditions
1 and 2 are satisfied? If the system is in equilibrium at absolute temperature
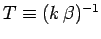 then it is distributed according to the Boltzmann
distribution. In the classical approximation,
the mean value of
then it is distributed according to the Boltzmann
distribution. In the classical approximation,
the mean value of 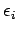 is expressed in terms of
integrals over all phase-space:
is expressed in terms of
integrals over all phase-space:
![\begin{displaymath}
\overline{\epsilon_i} = \frac{
\int_{-\infty}^{\infty} \exp[...
...}^{\infty} \exp[-\beta E(q_1,\cdots, p_f)]\,
dq_1\cdots dp_f}.
\end{displaymath}](img1071.png) |
(458) |
Condition 1 gives
where use has been made of the multiplicative property of the exponential function,
and where the last integrals in both the numerator and denominator extend over
all variables
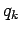 and
and  except
except 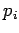 . These integrals are equal and, thus, cancel.
Hence,
. These integrals are equal and, thus, cancel.
Hence,
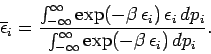 |
(460) |
This expression can be simplified further since
![\begin{displaymath}
\int_{-\infty}^\infty
\exp(-\beta \,\epsilon_i)\,\epsilon_i...
...\int_{-\infty}^\infty \exp(-\beta \,\epsilon_i)\, dp_i\right],
\end{displaymath}](img1076.png) |
(461) |
so
![\begin{displaymath}
\overline{\epsilon}_i = - \frac{\partial}{\partial\beta}
\l...
...int_{-\infty}^\infty \exp(-\beta \,\epsilon_i)\,
dp_i\right].
\end{displaymath}](img1077.png) |
(462) |
According to condition 2,
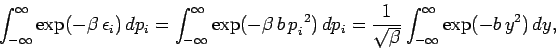 |
(463) |
where
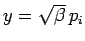 . Thus,
. Thus,
 |
(464) |
Note that the integral on the right-hand side does not depend on 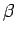 at all. It follows
from Eq. (462) that
at all. It follows
from Eq. (462) that
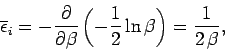 |
(465) |
giving
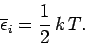 |
(466) |
This is the famous equipartition theorem of classical physics.
It states that the mean value of every independent
quadratic term in the energy is equal to  . If all terms in the energy are quadratic
then the mean energy is spread equally over all degrees of freedom (hence the
name ``equipartition'').
. If all terms in the energy are quadratic
then the mean energy is spread equally over all degrees of freedom (hence the
name ``equipartition'').



Next: Harmonic oscillators
Up: Applications of statistical thermodynamics
Previous: Gibb's paradox
Richard Fitzpatrick
2006-02-02
![]() generalized coordinates
generalized coordinates ![]() and corresponding
and corresponding ![]() generalized momenta
generalized momenta ![]() , so that
, so that
![]() in thermal equilibrium if conditions
1 and 2 are satisfied? If the system is in equilibrium at absolute temperature
in thermal equilibrium if conditions
1 and 2 are satisfied? If the system is in equilibrium at absolute temperature
![]() then it is distributed according to the Boltzmann
distribution. In the classical approximation,
the mean value of
then it is distributed according to the Boltzmann
distribution. In the classical approximation,
the mean value of ![]() is expressed in terms of
integrals over all phase-space:
is expressed in terms of
integrals over all phase-space:
![\begin{displaymath}
\overline{\epsilon_i} = \frac{
\int_{-\infty}^{\infty} \exp[...
...}^{\infty} \exp[-\beta E(q_1,\cdots, p_f)]\,
dq_1\cdots dp_f}.
\end{displaymath}](img1071.png)
![$\displaystyle \frac{
\int_{-\infty}^{\infty} \exp[-\beta\,(\epsilon_i + E')]\,
...
...p_f}
{\int_{-\infty}^{\infty} \exp[-\beta\,(\epsilon_i + E')]\,dq_1\cdots dp_f}$](img1073.png)
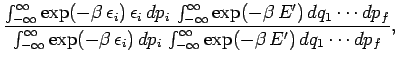
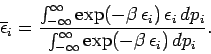
![\begin{displaymath}
\int_{-\infty}^\infty
\exp(-\beta \,\epsilon_i)\,\epsilon_i...
...\int_{-\infty}^\infty \exp(-\beta \,\epsilon_i)\, dp_i\right],
\end{displaymath}](img1076.png)