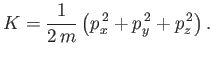 |
(7.161) |
Suppose that our gas is contained in a cubic enclosure of dimensions ![]() . According
to Schrödinger's equation, the quantized translational
energy levels of an individual molecule are given by
. According
to Schrödinger's equation, the quantized translational
energy levels of an individual molecule are given by
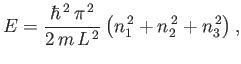 |
(7.163) |
The electronic degrees of freedom of gas molecules (i.e., the possible
configurations of electrons orbiting the atomic nuclei) typically give rise
to absorption and emission in the
ultraviolet or visible regions of the spectrum. It follows from Table 7.1 that
electronic degrees of freedom are frozen out at room temperature. Similarly,
nuclear degrees of freedom (i.e., the possible configurations of protons
and neutrons in the atomic nuclei) are frozen out because they are associated
with absorption and emission in the X-ray and ![]() -ray regions of the
electromagnetic spectrum. In fact, the only additional degrees of freedom
that we need worry about for gases are rotational and vibrational degrees of freedom.
These typically give rise to absorption lines in the infrared region of the
spectrum.
-ray regions of the
electromagnetic spectrum. In fact, the only additional degrees of freedom
that we need worry about for gases are rotational and vibrational degrees of freedom.
These typically give rise to absorption lines in the infrared region of the
spectrum.
The rotational kinetic energy of a molecule tumbling in space can be written
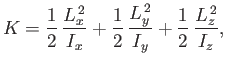 |
(7.164) |
 |
(7.165) |
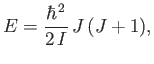 |
(7.166) |
Classically, the vibrational degrees of freedom of a molecule are studied by
standard normal mode analysis of the
molecular
structure. Each normal mode behaves like an
independent harmonic oscillator, and, therefore,
contributes ![]() to the molar specific heat of the gas [
to the molar specific heat of the gas [![]() from the
kinetic energy of vibration, and
from the
kinetic energy of vibration, and ![]() from the potential energy of
vibration]. A molecule containing
from the potential energy of
vibration]. A molecule containing ![]() atoms has
atoms has ![]() normal modes of vibration.
For instance, a diatomic molecule has just one normal mode (corresponding to
periodic stretching of the bond between the two atoms). Thus, the classical
contribution to the specific heat from vibrational degrees of freedom is
normal modes of vibration.
For instance, a diatomic molecule has just one normal mode (corresponding to
periodic stretching of the bond between the two atoms). Thus, the classical
contribution to the specific heat from vibrational degrees of freedom is
| (7.167) |
So, do any of the rotational and vibrational degrees of freedom
actually make a contribution to the specific heats of gases at room temperature,
once quantum effects have been taken into consideration? We can answer this
question by
examining just one piece of data. Figure 7.3 shows the
infrared absorption spectrum of hydrogen chloride gas. The absorption lines correspond
to simultaneous transitions between different vibrational and rotational energy
levels. Hence, this is usually called a vibration-rotation spectrum. The missing
line at about ![]() microns corresponds to a pure vibrational transition from the
ground-state to the first excited state.
(Pure vibrational transitions are
forbidden--hydrogen chloride molecules always have to simultaneously change their rotational energy level if they are to couple effectively to electromagnetic radiation.)
The longer wavelength absorption lines correspond to vibrational transitions in
which there is a simultaneous decrease in the rotational energy level.
Likewise, the
shorter wavelength absorption lines correspond to vibrational transitions in which
there is a simultaneous increase in the rotational energy level. It is clear that
the rotational energy levels are more closely spaced than the vibrational energy
levels. The pure vibrational transition gives rise to absorption at
about
microns corresponds to a pure vibrational transition from the
ground-state to the first excited state.
(Pure vibrational transitions are
forbidden--hydrogen chloride molecules always have to simultaneously change their rotational energy level if they are to couple effectively to electromagnetic radiation.)
The longer wavelength absorption lines correspond to vibrational transitions in
which there is a simultaneous decrease in the rotational energy level.
Likewise, the
shorter wavelength absorption lines correspond to vibrational transitions in which
there is a simultaneous increase in the rotational energy level. It is clear that
the rotational energy levels are more closely spaced than the vibrational energy
levels. The pure vibrational transition gives rise to absorption at
about ![]() microns, which corresponds to infrared radiation of frequency
microns, which corresponds to infrared radiation of frequency
![]() hertz with an associated
radiation ``temperature'' of 4,100K. We
conclude that
the vibrational degrees of freedom of hydrogen chloride, or any other small molecule,
are frozen out at room temperature. The rotational transitions split the
vibrational lines by about
hertz with an associated
radiation ``temperature'' of 4,100K. We
conclude that
the vibrational degrees of freedom of hydrogen chloride, or any other small molecule,
are frozen out at room temperature. The rotational transitions split the
vibrational lines by about ![]() microns. This implies that pure rotational
transitions would be associated with infrared radiation of frequency
microns. This implies that pure rotational
transitions would be associated with infrared radiation of frequency
![]() hertz and corresponding
radiation ``temperature'' 240K. We
conclude that the rotational degrees of freedom of hydrogen chloride, or any other small
molecule, are not frozen out at room temperature, and probably contribute the
classical
hertz and corresponding
radiation ``temperature'' 240K. We
conclude that the rotational degrees of freedom of hydrogen chloride, or any other small
molecule, are not frozen out at room temperature, and probably contribute the
classical ![]() to the molar specific heat. There is one proviso, however.
Linear molecules (like hydrogen chloride) effectively only have two rotational degrees of
freedom (instead of the usual three), because of the very small moment
of inertia of such molecules along the line of centers of the atoms.
to the molar specific heat. There is one proviso, however.
Linear molecules (like hydrogen chloride) effectively only have two rotational degrees of
freedom (instead of the usual three), because of the very small moment
of inertia of such molecules along the line of centers of the atoms.
We are now in a position to make some predictions regarding the specific heats
of various gases. Monatomic molecules only possess three translational degrees
of freedom, so monatomic gases should have a molar heat capacity
![]() joules/degree/mole. Moreover, the ratio of specific heats
joules/degree/mole. Moreover, the ratio of specific heats
![]() should be
should be
![]() . It can be seen from Table 6.1 that both of
these predictions are borne out pretty well for helium and argon.
Diatomic molecules possess three translational degrees of freedom, and
two rotational degrees of freedom. (All other degrees of freedom are frozen out
at room temperature.) Thus, diatomic gases should have a molar heat capacity
. It can be seen from Table 6.1 that both of
these predictions are borne out pretty well for helium and argon.
Diatomic molecules possess three translational degrees of freedom, and
two rotational degrees of freedom. (All other degrees of freedom are frozen out
at room temperature.) Thus, diatomic gases should have a molar heat capacity
![]() joules/degree/mole. Moreover, the ratio of specific heats should be
joules/degree/mole. Moreover, the ratio of specific heats should be
![]() . It can be seen from Table 6.1 that these are reasonably accurate
predictions for nitrogen and oxygen. The freezing out of vibrational
degrees of freedom becomes gradually less effective as molecules become heavier
and more complex. This is partly because such molecules are generally less
stable, so the force constant,
. It can be seen from Table 6.1 that these are reasonably accurate
predictions for nitrogen and oxygen. The freezing out of vibrational
degrees of freedom becomes gradually less effective as molecules become heavier
and more complex. This is partly because such molecules are generally less
stable, so the force constant, ![]() , is reduced, and partly
because the molecular mass
is increased. Both these effects reduce the frequency of vibration of the
molecular normal
modes [see Equation (7.141)], and, hence, the spacing between vibrational energy levels
[see Equation (7.140)]. This accounts for the obviously non-classical [i.e., not
a multiple of
, is reduced, and partly
because the molecular mass
is increased. Both these effects reduce the frequency of vibration of the
molecular normal
modes [see Equation (7.141)], and, hence, the spacing between vibrational energy levels
[see Equation (7.140)]. This accounts for the obviously non-classical [i.e., not
a multiple of ![]() ] specific heats of carbon dioxide and ethane in
Table 6.1.
In both molecules, vibrational degrees of freedom contribute to the molar specific
heat. (But not the full
] specific heats of carbon dioxide and ethane in
Table 6.1.
In both molecules, vibrational degrees of freedom contribute to the molar specific
heat. (But not the full ![]() , because the temperature is not sufficiently high.)
, because the temperature is not sufficiently high.)
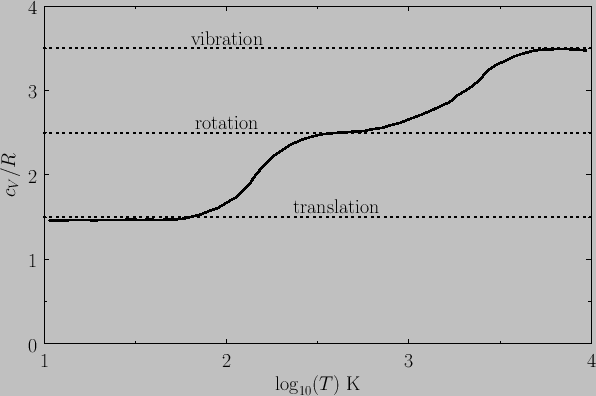 |
Figure 7.4 shows the variation of the molar heat capacity at constant volume
of gaseous molecular hydrogen (i.e., ![]() ) with temperature. The expected contribution
from the translational degrees of freedom is
) with temperature. The expected contribution
from the translational degrees of freedom is ![]() (there are
three translational degrees of freedom per molecule). The
expected contribution at
high temperatures from the rotational degrees of freedom is
(there are
three translational degrees of freedom per molecule). The
expected contribution at
high temperatures from the rotational degrees of freedom is ![]() (there are effectively
two rotational degrees of freedom per molecule). Finally, the expected contribution at high temperatures from the vibrational degrees of freedom is
(there are effectively
two rotational degrees of freedom per molecule). Finally, the expected contribution at high temperatures from the vibrational degrees of freedom is ![]() (there
is one vibrational degree of freedom per molecule). It can be seen that,
as the temperature rises, the rotational, and then the vibrational, degrees
of freedom eventually make their full classical contributions to the heat
capacity.
(there
is one vibrational degree of freedom per molecule). It can be seen that,
as the temperature rises, the rotational, and then the vibrational, degrees
of freedom eventually make their full classical contributions to the heat
capacity.