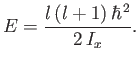Next: About this document ...
Up: Wave Mechanics
Previous: Simple Harmonic Oscillator
Angular Momentum
In classical mechanics, the vector angular momentum, L, of a particle of
position vector 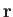 and linear momentum
and linear momentum
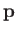 is defined as
is defined as
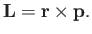 |
(C.122) |
In other words,
In quantum mechanics, the operators,  , that represent
the Cartesian components of linear momentum, are represented
as the spatial differential operators
, that represent
the Cartesian components of linear momentum, are represented
as the spatial differential operators
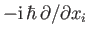 . [See Equation (C.81)].
It follows that:
. [See Equation (C.81)].
It follows that:
In addition, let
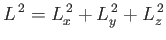 |
(C.129) |
be the magnitude-squared of the angular momentum vector.
It is most convenient to work in terms of the standard
spherical coordinates,  ,
, 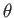 , and
, and 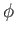 . These are
defined with respect to our usual Cartesian coordinates as follows:
. These are
defined with respect to our usual Cartesian coordinates as follows:
We deduce, after some tedious analysis, that
Making use of the definitions (C.126)-(C.129), after more tedious algebra, we obtain
as well as
![$\displaystyle L^2 = -\hbar^{ 2}\left[\frac{1}{\sin\theta}\frac{\partial}{\part...
...ight) + \frac{1}{\sin^2\theta}\frac{\partial^{ 2}}{\partial\phi^{ 2}}\right].$](img3322.png) |
(C.139) |
We, thus, conclude that all of our angular momentum operators can be represented
as differential operators involving the angular spherical
coordinates, 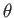 and
and 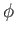 , but not involving the radial coordinate,
, but not involving the radial coordinate,
 .
.
Let us search for an angular wavefunction,
 , that is a simultaneous eigenstate of
, that is a simultaneous eigenstate of  and
and 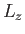 .
In other words,
.
In other words,
where 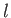 and
and  are dimensionless constants. We also want the wavefunction to satisfy the normalization constraint
are dimensionless constants. We also want the wavefunction to satisfy the normalization constraint
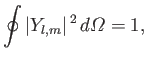 |
(C.142) |
where
 is an element of solid angle, and the integral is over all solid angle.
Thus, we are searching for well-behaved angular functions that simultaneously satisfy,
is an element of solid angle, and the integral is over all solid angle.
Thus, we are searching for well-behaved angular functions that simultaneously satisfy,
As is well known, the requisite functions are the so-called spherical harmonics,
![$\displaystyle Y_{l,m}(\theta,\phi) =(-1)^{ m} \left[\frac{2 l+1}{4\pi} \frac{(l-m)!}{(l+m)!}\right]^{1/2} P_{l,m}(\cos\theta) {\rm e}^{ {\rm i} m \phi},$](img3337.png) |
(C.146) |
for 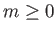 .
Here, the
.
Here, the 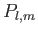 are known as associated Legendre
polynomials, and are written
are known as associated Legendre
polynomials, and are written
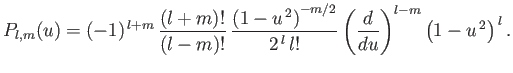 |
(C.147) |
for 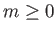 .
Note that
.
Note that
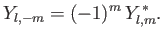 |
(C.148) |
Finally, the constant 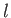 is constrained to take non-negative integer values, whereas the constant
is constrained to take non-negative integer values, whereas the constant  is constrained to take
integer values in the range
is constrained to take
integer values in the range
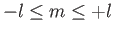 . Thus,
. Thus, 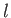 is a quantum number that determines the value of
is a quantum number that determines the value of  . In fact,
. In fact,
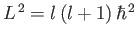 . Likewise,
. Likewise,  is a quantum number that determines the value of
is a quantum number that determines the value of 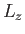 . In fact,
. In fact,
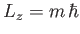 .
.
The classical Hamiltonian of an extended object spinning with constant angular momentum 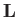 about one of its principal
axes of rotation is
about one of its principal
axes of rotation is
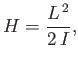 |
(C.149) |
where  is the associated principal moment of inertia. Let us assume that the quantum-mechanical Hamiltonian of an object spinning
about a principal axis of rotation has the
same form. We can solve the energy eigenvalue problem,
is the associated principal moment of inertia. Let us assume that the quantum-mechanical Hamiltonian of an object spinning
about a principal axis of rotation has the
same form. We can solve the energy eigenvalue problem,
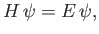 |
(C.150) |
by writing
 , where
, where  is arbitrary. It immediately follows from Equation (C.140) that
is arbitrary. It immediately follows from Equation (C.140) that
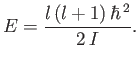 |
(C.151) |
In other words, the energy levels are quantized in terms of the quantum number, 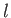 , that specifies the value of
, that specifies the value of  .
.
The classical Hamiltonian of an extended object spinning about a general axis is
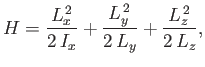 |
(C.152) |
where the Cartesian axes are aligned along the body's principal axes of rotation, and 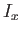 ,
, 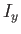 ,
,  are
the corresponding principal moments of inertia. Suppose that the body is axially symmetric about the
are
the corresponding principal moments of inertia. Suppose that the body is axially symmetric about the
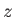 -axis. It follows that
-axis. It follows that 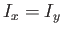 . The previous Hamiltonian can be written
. The previous Hamiltonian can be written
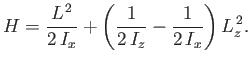 |
(C.153) |
Let us assume that the quantum-mechanical Hamiltonian of an axisymmetric object spinning about an arbitrary axis
has the same form as the previous Hamiltonian. We can solve the energy eigenvalue problem,
 , by
writing
, by
writing
 , where
, where  is arbitrary. It immediately follows from
Equations (C.140) and (C.141) that
is arbitrary. It immediately follows from
Equations (C.140) and (C.141) that
![$\displaystyle E = \frac{[l (l+1)-m^{ 2}] \hbar^{ 2}}{2 I_x} + \frac{m^{ 2} \hbar^{ 2}}{2 I_z}.$](img3354.png) |
(C.154) |
In other words, the energy levels are quantized in terms of the quantum number, 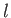 , that specifies the value of
, that specifies the value of  , as
well as the quantum number,
, as
well as the quantum number,  , that determines the value of
, that determines the value of 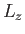 . If
. If
 (in other words, if the
object is highly elongated along its symmetry axis) then the spacing between energy levels corresponding to
different values of
(in other words, if the
object is highly elongated along its symmetry axis) then the spacing between energy levels corresponding to
different values of  becomes much greater than the spacing between energy levels corresponding to
different values of
becomes much greater than the spacing between energy levels corresponding to
different values of 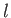 . In this case, it is plausible that the system remains in the
. In this case, it is plausible that the system remains in the 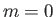 state (because
it cannot acquire sufficient energy to reach the
state (because
it cannot acquire sufficient energy to reach the 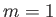 state), so that
state), so that
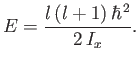 |
(C.155) |



Next: About this document ...
Up: Wave Mechanics
Previous: Simple Harmonic Oscillator
Richard Fitzpatrick
2016-01-25
![]() , that represent
the Cartesian components of linear momentum, are represented
as the spatial differential operators
, that represent
the Cartesian components of linear momentum, are represented
as the spatial differential operators
![]() . [See Equation (C.81)].
It follows that:
. [See Equation (C.81)].
It follows that:
![]() ,
, ![]() , and
, and ![]() . These are
defined with respect to our usual Cartesian coordinates as follows:
. These are
defined with respect to our usual Cartesian coordinates as follows:

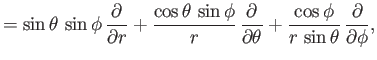

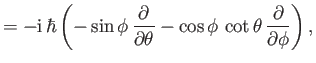
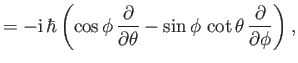

![$\displaystyle L^2 = -\hbar^{ 2}\left[\frac{1}{\sin\theta}\frac{\partial}{\part...
...ight) + \frac{1}{\sin^2\theta}\frac{\partial^{ 2}}{\partial\phi^{ 2}}\right].$](img3322.png)
![]() , that is a simultaneous eigenstate of
, that is a simultaneous eigenstate of ![]() and
and ![]() .
In other words,
.
In other words,
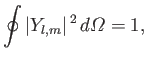
![$\displaystyle \left[\frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left( \...
...+ \frac{1}{\sin^2\theta}\frac{\partial^{ 2}}{\partial\phi^{ 2}}\right]Y_{l,m}$](img3331.png)
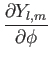
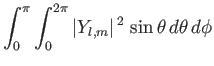
![$\displaystyle Y_{l,m}(\theta,\phi) =(-1)^{ m} \left[\frac{2 l+1}{4\pi} \frac{(l-m)!}{(l+m)!}\right]^{1/2} P_{l,m}(\cos\theta) {\rm e}^{ {\rm i} m \phi},$](img3337.png)
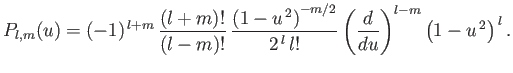
![]() about one of its principal
axes of rotation is
about one of its principal
axes of rotation is
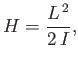
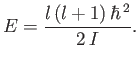
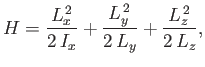
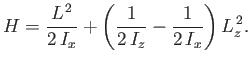
![$\displaystyle E = \frac{[l (l+1)-m^{ 2}] \hbar^{ 2}}{2 I_x} + \frac{m^{ 2} \hbar^{ 2}}{2 I_z}.$](img3354.png)