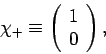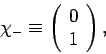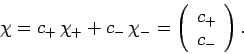

Next: Spin Precession
Up: Spin Angular Momentum
Previous: Eigenstates of and
Pauli Representation
Let us denote the two independent spin eigenstates of an electron as
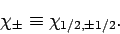 |
(734) |
It thus follows, from Eqs. (717) and (718), that
Note that 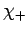 corresponds to an electron whose spin angular momentum vector has a positive component along the
corresponds to an electron whose spin angular momentum vector has a positive component along the 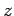 -axis. Loosely speaking,
we could say that the spin vector points in the
-axis. Loosely speaking,
we could say that the spin vector points in the 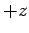 -direction (or its spin is
``up''). Likewise,
-direction (or its spin is
``up''). Likewise,
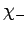 corresponds to an electron whose spin points in the
corresponds to an electron whose spin points in the 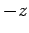 -direction
(or whose spin is ``down'').
These two eigenstates satisfy the orthonormality requirements
-direction
(or whose spin is ``down'').
These two eigenstates satisfy the orthonormality requirements
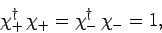 |
(737) |
and
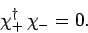 |
(738) |
A general spin state can be represented as a linear combination of
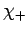 and
and 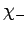 : i.e.,
: i.e.,
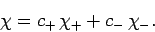 |
(739) |
It is thus evident that electron spin space is two-dimensional.
Up to now, we have discussed spin space in rather abstract terms. In the
following, we shall describe a particular representation of electron
spin space due to Pauli. This so-called Pauli representation allows us
to visualize spin space, and also facilitates calculations involving spin.
Let us attempt to represent a general spin state as a complex column vector in some two-dimensional space: i.e.,
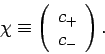 |
(740) |
The corresponding dual vector is represented as a row vector: i.e.,
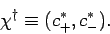 |
(741) |
Furthermore, the product
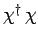 is obtained according to the
ordinary rules of matrix multiplication: i.e.,
is obtained according to the
ordinary rules of matrix multiplication: i.e.,
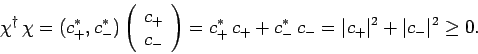 |
(742) |
Likewise, the product
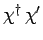 of two different spin states
is also obtained from the rules of matrix multiplication: i.e.,
of two different spin states
is also obtained from the rules of matrix multiplication: i.e.,
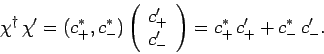 |
(743) |
Note that this particular representation of spin space is in complete accordance with the discussion in Sect. 10.3. For obvious reasons,
a vector used to represent a spin state is generally known as
spinor.
A general spin operator 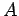 is represented as a
is represented as a 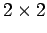 matrix
which operates on a spinor: i.e.,
matrix
which operates on a spinor: i.e.,
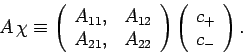 |
(744) |
As is easily demonstrated, the Hermitian conjugate of 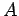 is represented by
the transposed complex conjugate of the matrix used to represent
is represented by
the transposed complex conjugate of the matrix used to represent 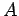 : i.e.,
: i.e.,
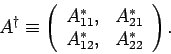 |
(745) |
Let us represent the spin eigenstates 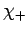 and
and 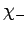 as
as
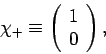 |
(746) |
and
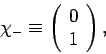 |
(747) |
respectively. Note that these forms automatically
satisfy the orthonormality constraints (737) and (738).
It is convenient to write the spin operators 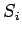 (where
(where 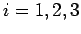 corresponds to
corresponds to
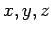 ) as
) as
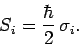 |
(748) |
Here, the 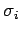 are dimensionless
are dimensionless 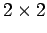 matrices. According
to Eqs. (702)-(704), the
matrices. According
to Eqs. (702)-(704), the 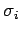 satisfy the commutation
relations
satisfy the commutation
relations
Furthermore, Eq. (735) yields
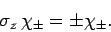 |
(752) |
It is easily demonstrated, from the above expressions, that the 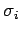 are represented by the
following matrices:
are represented by the
following matrices:
Incidentally, these matrices are generally known as the Pauli matrices.
Finally, a general spinor takes the form
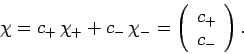 |
(756) |
If the spinor is properly normalized then
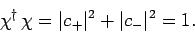 |
(757) |
In this case, we can interpret 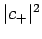 as the probability that
an observation of
as the probability that
an observation of  will yield the result
will yield the result 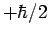 , and
, and
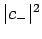 as the probability that an observation of
as the probability that an observation of 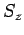 will yield the result
will yield the result 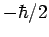 .
.


Next: Spin Precession
Up: Spin Angular Momentum
Previous: Eigenstates of and
Richard Fitzpatrick
2010-07-20
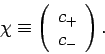
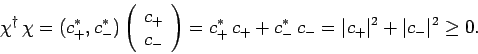
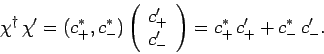
![]() is represented as a
is represented as a ![]() matrix
which operates on a spinor: i.e.,
matrix
which operates on a spinor: i.e.,
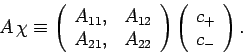
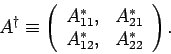
![]() and
and ![]() as
as