


Next: Spin Space
Up: Spin Angular Momentum
Previous: Introduction
Spin Operators
Since spin is a type of angular momentum, it is reasonable to suppose
that it possesses similar properties to orbital angular momentum.
Thus, by analogy with Sect. 8.2, we would expect to be able
to define three operators--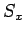 ,
, 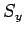 , and
, and  --which represent
the three Cartesian components of spin angular momentum. Moreover,
it is plausible that these operators
possess
analogous commutation relations to the three corresponding orbital
angular momentum operators,
--which represent
the three Cartesian components of spin angular momentum. Moreover,
it is plausible that these operators
possess
analogous commutation relations to the three corresponding orbital
angular momentum operators, 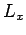 ,
, 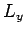 , and
, and 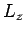 [see Eqs. (531)-(533)]. In other words,
[see Eqs. (531)-(533)]. In other words,
We can represent the magnitude squared of the spin angular momentum vector by the operator
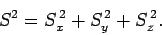 |
(705) |
By analogy with the analysis in Sect. 8.2, it is
easily demonstrated that
![\begin{displaymath}[S^2, S_x]= [S^2, S_y] = [S^2,S_z] = 0.
\end{displaymath}](img1707.png) |
(706) |
We thus conclude (see Sect. 4.10) that we can simultaneously measure the magnitude squared
of the spin angular momentum vector, together with, at most, one Cartesian component.
By convention, we shall always choose to measure the 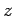 -component,
-component,  .
.
By analogy with Eq. (538), we can define raising and lowering
operators for spin angular momentum:
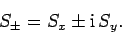 |
(707) |
If 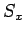 ,
, 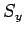 , and
, and  are Hermitian operators, as must be
the case if they are to represent physical quantities, then
are Hermitian operators, as must be
the case if they are to represent physical quantities, then 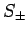 are
the Hermitian conjugates of one another: i.e.,
are
the Hermitian conjugates of one another: i.e.,
 |
(708) |
Finally, by analogy with Sect. 8.2, it is easily
demonstrated that



Next: Spin Space
Up: Spin Angular Momentum
Previous: Introduction
Richard Fitzpatrick
2010-07-20