


Next: Derivation of Radial Equation
Up: Central Potentials
Previous: Central Potentials
In this chapter, we shall investigate the interaction of a non-relativistic
particle of mass 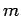 and energy
and energy 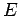 with various so-called central potentials,
with various so-called central potentials,
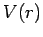 , where
, where
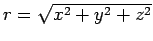 is the radial distance from the origin.
It is, of course, most convenient
to work in spherical polar coordinates--
is the radial distance from the origin.
It is, of course, most convenient
to work in spherical polar coordinates--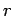 ,
,  ,
, 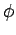 --during such an investigation (see Sect. 8.3). Thus, we shall be searching for stationary
wavefunctions,
--during such an investigation (see Sect. 8.3). Thus, we shall be searching for stationary
wavefunctions,
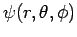 , which satisfy the time-independent
Schrödinger equation (see Sect. 4.12)
, which satisfy the time-independent
Schrödinger equation (see Sect. 4.12)
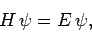 |
(622) |
where the Hamiltonian takes the standard non-relativistic form
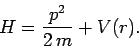 |
(623) |
Richard Fitzpatrick
2010-07-20