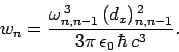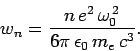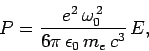Next: Selection Rules
Up: Time-Dependent Perturbation Theory
Previous: Spontaneous Emission
Consider an electron in a one-dimensional harmonic oscillator
potential aligned along the  -axis. According to Sect. 5.8, the
unperturbed energy eigenvalues of the system are
-axis. According to Sect. 5.8, the
unperturbed energy eigenvalues of the system are
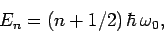 |
(1135) |
where 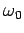 is the frequency of the corresponding classical
oscillator. Here, the quantum number
is the frequency of the corresponding classical
oscillator. Here, the quantum number 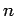 takes the values
takes the values  .
Let the
.
Let the 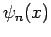 be the (real) properly normalized unperturbed eigenstates of the system.
be the (real) properly normalized unperturbed eigenstates of the system.
Suppose that the electron is initially in an excited state: i.e.,  . In principle, the electron can decay to a lower energy state via
the spontaneous emission of a photon of the appropriate frequency.
Let us investigate this effect. Now, according to Eq. (1131),
the system can only make a spontaneous transition from an
energy state corresponding to the quantum number
. In principle, the electron can decay to a lower energy state via
the spontaneous emission of a photon of the appropriate frequency.
Let us investigate this effect. Now, according to Eq. (1131),
the system can only make a spontaneous transition from an
energy state corresponding to the quantum number 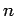 to one
corresponding to the quantum number
to one
corresponding to the quantum number 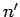 if the associated electric dipole moment
if the associated electric dipole moment
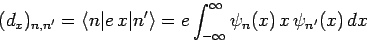 |
(1136) |
is non-zero [since
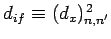 for the case in hand]. However, according
to Eq. (416),
for the case in hand]. However, according
to Eq. (416),
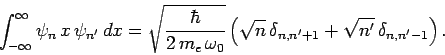 |
(1137) |
Since we are dealing with emission, we must have 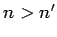 . Hence, we
obtain
. Hence, we
obtain
 |
(1138) |
It is clear that (in the electric dipole approximation) we can only have
spontaneous emission between states whose quantum numbers differ
by unity. Thus, the frequency of the photon emitted when the 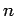 th excited
state decays is
th excited
state decays is
 |
(1139) |
Hence, we conclude that, no matter which state decays, the emitted photon always has the same frequency as the classical oscillator.
According to Eq. (1131), the decay rate of the 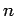 th excited
state is given by
th excited
state is given by
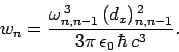 |
(1140) |
It follows that
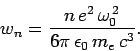 |
(1141) |
The mean radiated power is simply
![\begin{displaymath}
P_n = \hbar \omega_0 w_n = \frac{e^2 \omega_0^{ 2}}{6\pi \epsilon_0 m_e c^3} [E_n -(1/2) \hbar \omega_0].
\end{displaymath}](img2633.png) |
(1142) |
Classically, an electron in a one-dimensional oscillator potential
radiates at the oscillation frequency 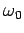 with the mean power
with the mean power
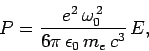 |
(1143) |
where 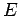 is the oscillator energy. It can be seen that a quantum
oscillator radiates in an almost exactly analogous manner to
the equivalent classical oscillator. The only difference is the
factor
is the oscillator energy. It can be seen that a quantum
oscillator radiates in an almost exactly analogous manner to
the equivalent classical oscillator. The only difference is the
factor
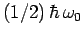 in Eq. (1142)--this is
needed to ensure that the ground-state of the quantum oscillator does not radiate.
in Eq. (1142)--this is
needed to ensure that the ground-state of the quantum oscillator does not radiate.



Next: Selection Rules
Up: Time-Dependent Perturbation Theory
Previous: Spontaneous Emission
Richard Fitzpatrick
2010-07-20
![]() . In principle, the electron can decay to a lower energy state via
the spontaneous emission of a photon of the appropriate frequency.
Let us investigate this effect. Now, according to Eq. (1131),
the system can only make a spontaneous transition from an
energy state corresponding to the quantum number
. In principle, the electron can decay to a lower energy state via
the spontaneous emission of a photon of the appropriate frequency.
Let us investigate this effect. Now, according to Eq. (1131),
the system can only make a spontaneous transition from an
energy state corresponding to the quantum number ![]() to one
corresponding to the quantum number
to one
corresponding to the quantum number ![]() if the associated electric dipole moment
if the associated electric dipole moment
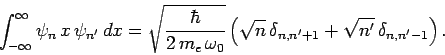

![]() th excited
state is given by
th excited
state is given by