


Next: Transitions in Hydrogen
Up: Time-Dependent Perturbation Theory
Previous: Radiation from a Harmonic
Let us now consider spontaneous transitions between the different energy levels
of a hydrogen atom. Since the perturbing Hamiltonian (1093) does
not contain any spin operators, we can neglect electron spin in our analysis.
Thus, according to Sect. 9.4, the various energy eigenstates of the
hydrogen atom are labeled by the familiar quantum numbers 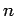 ,
, 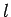 , and
, and
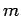 .
.
According to Eqs. (1122) and (1131), a hydrogen
atom can only make a spontaneous transition from an energy
state corresponding to the quantum numbers 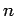 ,
, 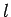 ,
, 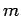 to
one corresponding to the quantum numbers
to
one corresponding to the quantum numbers 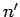 ,
, 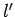 ,
, 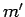 if
the modulus squared of the associated electric dipole moment
if
the modulus squared of the associated electric dipole moment
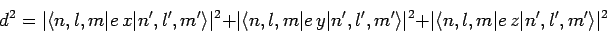 |
(1144) |
is non-zero. Now, we have already seen, in Sect. 12.5, that the
matrix element
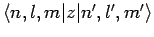 is only non-zero
provided that
is only non-zero
provided that  and
and 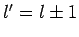 . It turns out that the proof
that this matrix element is zero unless
. It turns out that the proof
that this matrix element is zero unless 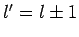 can, via a trivial modification, also be used to demonstrate
that
can, via a trivial modification, also be used to demonstrate
that
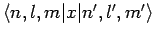 and
and
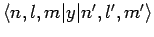 are also zero unless
are also zero unless 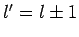 . Consider
. Consider
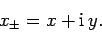 |
(1145) |
It is easily demonstrated that
![\begin{displaymath}[L_z, x_\pm]= \pm \hbar x_\pm.
\end{displaymath}](img2641.png) |
(1146) |
Hence,
![\begin{displaymath}
\langle n,l,m\vert[L_z,x_+]-\hbar x_+\vert n',l',m'\rangle...
...,(m-m'-1)
\langle n,l,m\vert x_+\vert n',l',m'\rangle = 0,
\end{displaymath}](img2642.png) |
(1147) |
and
![\begin{displaymath}
\langle n,l,m\vert[L_z,x_-]+\hbar x_-\vert n',l',m'\rangle...
...,(m-m'+1)
\langle n,l,m\vert x_-\vert n',l',m'\rangle = 0.
\end{displaymath}](img2643.png) |
(1148) |
Clearly,
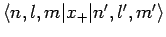 is zero unless
is zero unless 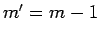 ,
and
,
and
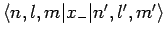 is zero unless
is zero unless 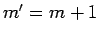 .
Now,
.
Now,
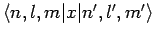 and
and
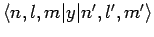 are
obviously both zero if
are
obviously both zero if
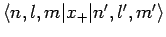 and
and
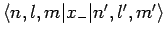 are both zero. Hence, we conclude that
are both zero. Hence, we conclude that
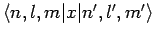 and
and
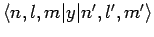 are only non-zero if
are only non-zero if  .
.
The above arguments demonstrate that spontaneous transitions between different energy levels of a hydrogen atom are only possible provided
These are termed the selection rules for electric dipole
transitions (i.e., transitions calculated using the electric
dipole approximation). Note, finally, that since the perturbing Hamiltonian
does not contain any spin operators, the spin quantum number 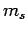 cannot change during a transition. Hence, we have the additional
selection rule that
cannot change during a transition. Hence, we have the additional
selection rule that 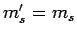 .
.



Next: Transitions in Hydrogen
Up: Time-Dependent Perturbation Theory
Previous: Radiation from a Harmonic
Richard Fitzpatrick
2010-07-20
![]() ,
, ![]() ,
, ![]() to
one corresponding to the quantum numbers
to
one corresponding to the quantum numbers ![]() ,
, ![]() ,
, ![]() if
the modulus squared of the associated electric dipole moment
if
the modulus squared of the associated electric dipole moment