Next: White-Dwarf Stars
Up: Three-Dimensional Quantum Mechanics
Previous: Particle in a Box
Consider 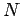 electrons trapped in a cubic box of dimension
electrons trapped in a cubic box of dimension 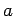 . Let us
treat the electrons as essentially non-interacting particles. According to Sect. 6.3,
the total energy of a system consisting of many non-interacting particles is simply the sum of the single-particle energies of the individual
particles. Furthermore, electrons are subject to
the Pauli exclusion principle (see Sect. 6.5), since
they are indistinguishable fermions. The exclusion principle
states that no two electrons in our system can occupy the same single-particle
energy level. Now, from the previous section, the single-particle
energy levels for a particle in a box are characterized by the three quantum numbers
. Let us
treat the electrons as essentially non-interacting particles. According to Sect. 6.3,
the total energy of a system consisting of many non-interacting particles is simply the sum of the single-particle energies of the individual
particles. Furthermore, electrons are subject to
the Pauli exclusion principle (see Sect. 6.5), since
they are indistinguishable fermions. The exclusion principle
states that no two electrons in our system can occupy the same single-particle
energy level. Now, from the previous section, the single-particle
energy levels for a particle in a box are characterized by the three quantum numbers
 ,
, 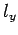 , and
, and 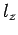 . Thus, we conclude that no two electrons in
our system can have the same set of values of
. Thus, we conclude that no two electrons in
our system can have the same set of values of  ,
, 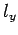 , and
, and 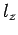 . It
turns out that this is not quite true, because electrons possess an intrinsic
angular momentum called spin (see Cha. 10). The spin states of an electron are
governed by an additional quantum number, which can take one of two different
values. Hence, when spin is taken into account, we conclude that
a maximum of two electrons (with different spin quantum numbers) can occupy
a single-particle energy level corresponding to a particular set of values of
. It
turns out that this is not quite true, because electrons possess an intrinsic
angular momentum called spin (see Cha. 10). The spin states of an electron are
governed by an additional quantum number, which can take one of two different
values. Hence, when spin is taken into account, we conclude that
a maximum of two electrons (with different spin quantum numbers) can occupy
a single-particle energy level corresponding to a particular set of values of  ,
, 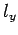 ,
and
,
and 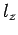 . Note, from Eqs. (504) and (505), that the associated particle energy is
proportional to
. Note, from Eqs. (504) and (505), that the associated particle energy is
proportional to
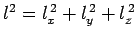 .
.
Suppose that our electrons are cold: i.e., they have comparatively
little thermal energy. In this case, we would expect them
to fill the lowest single-particle energy levels available to them. We can imagine the single-particle energy levels as existing in a sort of three-dimensional quantum number space whose Cartesian coordinates are
 ,
, 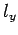 , and
, and 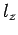 . Thus, the energy levels are uniformly
distributed in this space on a cubic lattice. Moreover, the distance between
nearest neighbour energy levels is unity. This implies that the
number of energy levels per unit volume is also unity. Finally, the energy of a given energy
level
is proportional to its distance,
. Thus, the energy levels are uniformly
distributed in this space on a cubic lattice. Moreover, the distance between
nearest neighbour energy levels is unity. This implies that the
number of energy levels per unit volume is also unity. Finally, the energy of a given energy
level
is proportional to its distance,
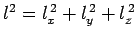 ,
from the origin.
,
from the origin.
Since we expect cold electrons to occupy the lowest energy levels
available to them, but only two electrons can occupy a given energy
level, it follows that if the number of electrons, 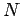 , is very large then
the filled energy levels will be approximately distributed in a sphere centered
on the origin of quantum number space. The number of energy levels contained in a sphere
of radius
, is very large then
the filled energy levels will be approximately distributed in a sphere centered
on the origin of quantum number space. The number of energy levels contained in a sphere
of radius 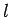 is approximately equal to the volume of the sphere--since
the number of energy levels per unit volume is unity. It turns out that this
is not quite correct, because we have forgotten that the quantum numbers
is approximately equal to the volume of the sphere--since
the number of energy levels per unit volume is unity. It turns out that this
is not quite correct, because we have forgotten that the quantum numbers
 ,
, 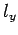 , and
, and 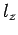 can only take positive values.
Hence, the filled energy levels actually only occupy one octant of a sphere.
The radius
can only take positive values.
Hence, the filled energy levels actually only occupy one octant of a sphere.
The radius 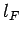 of the octant of filled energy levels in quantum number space can be calculated
by equating the number of energy levels it contains to the number of electrons,
of the octant of filled energy levels in quantum number space can be calculated
by equating the number of energy levels it contains to the number of electrons,
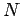 .
Thus, we can write
.
Thus, we can write
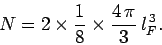 |
(506) |
Here, the factor 2 is to take into account the two spin states of an electron,
and the factor 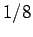 is to take account of the fact that
is to take account of the fact that  ,
, 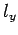 , and
, and 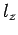 can only take positive values.
Thus,
can only take positive values.
Thus,
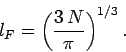 |
(507) |
According to Eq. (504), the energy of the most energetic
electrons--which is known as the Fermi energy--is given by
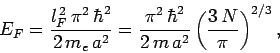 |
(508) |
where  is the electron mass.
This can also be written as
is the electron mass.
This can also be written as
 |
(509) |
where  is the number of electrons per unit volume (in real space). Note
that the Fermi energy only depends on the number density
of the confined electrons.
is the number of electrons per unit volume (in real space). Note
that the Fermi energy only depends on the number density
of the confined electrons.
The mean energy of the electrons is given by
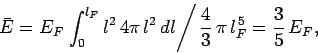 |
(510) |
since 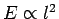 , and the energy levels are uniformly
distributed in quantum number space inside an octant of radius
, and the energy levels are uniformly
distributed in quantum number space inside an octant of radius 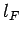 . Now, according to classical physics, the mean
thermal energy of the electrons is
. Now, according to classical physics, the mean
thermal energy of the electrons is 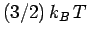 , where
, where  is the
electron temperature, and
is the
electron temperature, and 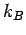 the
Boltzmann constant. Thus, if
the
Boltzmann constant. Thus, if 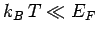 then our original assumption
that the electrons are cold is valid. Note that, in this case, the
electron energy is much larger than that predicted by classical
physics--electrons in this state are termed degenerate. On the
other hand, if
then our original assumption
that the electrons are cold is valid. Note that, in this case, the
electron energy is much larger than that predicted by classical
physics--electrons in this state are termed degenerate. On the
other hand, if 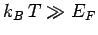 then the electrons are hot, and are essentially
governed by classical physics--electrons in this state are termed non-degenerate.
then the electrons are hot, and are essentially
governed by classical physics--electrons in this state are termed non-degenerate.
The total energy of a degenerate electron gas is
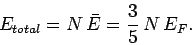 |
(511) |
Hence, the gas pressure takes the form
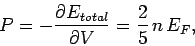 |
(512) |
since
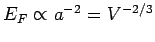 [see Eq. (508)].
Now, the pressure predicted by classical physics is
[see Eq. (508)].
Now, the pressure predicted by classical physics is 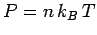 .
Thus, a degenerate electron gas has a much higher pressure than
that which would be predicted by classical physics. This is an entirely
quantum mechanical effect, and is due to the fact that identical fermions
cannot get significantly closer together than a de Broglie wavelength
without violating the Pauli exclusion principle. Note that, according to
Eq. (509), the mean spacing between degenerate electrons is
.
Thus, a degenerate electron gas has a much higher pressure than
that which would be predicted by classical physics. This is an entirely
quantum mechanical effect, and is due to the fact that identical fermions
cannot get significantly closer together than a de Broglie wavelength
without violating the Pauli exclusion principle. Note that, according to
Eq. (509), the mean spacing between degenerate electrons is
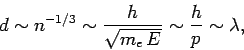 |
(513) |
where 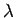 is the de Broglie wavelength. Thus, an electron gas
is non-degenerate when the mean spacing between the electrons is much
greater than the de Broglie wavelength, and becomes degenerate as the
mean spacing approaches the de Broglie wavelength.
is the de Broglie wavelength. Thus, an electron gas
is non-degenerate when the mean spacing between the electrons is much
greater than the de Broglie wavelength, and becomes degenerate as the
mean spacing approaches the de Broglie wavelength.
In turns out that the conduction (i.e., free) electrons inside metals are
highly degenerate (since the number of electrons per unit volume
is very large, and
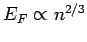 ). Indeed, most metals are hard to compress
as a direct consequence of the high degeneracy pressure of their conduction
electrons. To be more exact, resistance to compression is usually measured
in terms of a quantity known as the bulk modulus, which is defined
). Indeed, most metals are hard to compress
as a direct consequence of the high degeneracy pressure of their conduction
electrons. To be more exact, resistance to compression is usually measured
in terms of a quantity known as the bulk modulus, which is defined
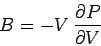 |
(514) |
Now, for a fixed number of electrons,
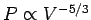 [see Eqs. (508) and (512)]. Hence,
[see Eqs. (508) and (512)]. Hence,
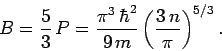 |
(515) |
For example, the number density of free electrons in magnesium is
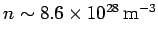 . This leads to the following estimate
for the bulk modulus:
. This leads to the following estimate
for the bulk modulus:
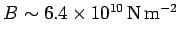 .
The actual bulk modulus is
.
The actual bulk modulus is
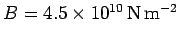 .
.



Next: White-Dwarf Stars
Up: Three-Dimensional Quantum Mechanics
Previous: Particle in a Box
Richard Fitzpatrick
2010-07-20
![]() ,
, ![]() , and
, and ![]() . Thus, the energy levels are uniformly
distributed in this space on a cubic lattice. Moreover, the distance between
nearest neighbour energy levels is unity. This implies that the
number of energy levels per unit volume is also unity. Finally, the energy of a given energy
level
is proportional to its distance,
. Thus, the energy levels are uniformly
distributed in this space on a cubic lattice. Moreover, the distance between
nearest neighbour energy levels is unity. This implies that the
number of energy levels per unit volume is also unity. Finally, the energy of a given energy
level
is proportional to its distance,
![]() ,
from the origin.
,
from the origin.
![]() , is very large then
the filled energy levels will be approximately distributed in a sphere centered
on the origin of quantum number space. The number of energy levels contained in a sphere
of radius
, is very large then
the filled energy levels will be approximately distributed in a sphere centered
on the origin of quantum number space. The number of energy levels contained in a sphere
of radius ![]() is approximately equal to the volume of the sphere--since
the number of energy levels per unit volume is unity. It turns out that this
is not quite correct, because we have forgotten that the quantum numbers
is approximately equal to the volume of the sphere--since
the number of energy levels per unit volume is unity. It turns out that this
is not quite correct, because we have forgotten that the quantum numbers
![]() ,
, ![]() , and
, and ![]() can only take positive values.
Hence, the filled energy levels actually only occupy one octant of a sphere.
The radius
can only take positive values.
Hence, the filled energy levels actually only occupy one octant of a sphere.
The radius ![]() of the octant of filled energy levels in quantum number space can be calculated
by equating the number of energy levels it contains to the number of electrons,
of the octant of filled energy levels in quantum number space can be calculated
by equating the number of energy levels it contains to the number of electrons,
![]() .
Thus, we can write
.
Thus, we can write
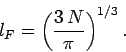
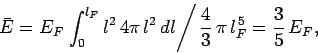
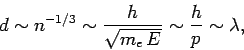
![]() ). Indeed, most metals are hard to compress
as a direct consequence of the high degeneracy pressure of their conduction
electrons. To be more exact, resistance to compression is usually measured
in terms of a quantity known as the bulk modulus, which is defined
). Indeed, most metals are hard to compress
as a direct consequence of the high degeneracy pressure of their conduction
electrons. To be more exact, resistance to compression is usually measured
in terms of a quantity known as the bulk modulus, which is defined