Next: Two-Particle Systems
Up: Multi-Particle Systems
Previous: Fundamental Concepts
Non-Interacting Particles
In general, we expect the Hamiltonian of a multi-particle system to take the form
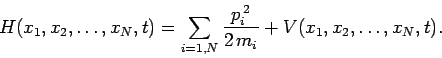 |
(426) |
Here, the first term on the right-hand side represents the total kinetic
energy of the system, whereas the potential 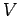 specifies the nature of the interaction between the
various particles making up the system, as well as the interaction of the
particles with any external forces.
specifies the nature of the interaction between the
various particles making up the system, as well as the interaction of the
particles with any external forces.
Suppose that the particles do not interact with one another. This
implies that each particle moves in a common potential: i.e.,
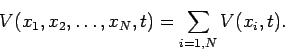 |
(427) |
Hence, we can write
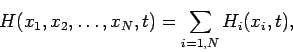 |
(428) |
where
 |
(429) |
In other words, for the case of non-interacting particles, the
multi-particle Hamiltonian of the system can be written as the
sum of 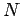 independent single-particle Hamiltonians. Here,
independent single-particle Hamiltonians. Here, 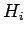 represents the energy of the
represents the energy of the  th particle, and is completely
unaffected by the energies of the other particles.
Furthermore, given that the various particles which make up the
system are non-interacting, we expect their instantaneous positions to be completely
uncorrelated with one another. This immediately implies that
the multi-particle wavefunction
th particle, and is completely
unaffected by the energies of the other particles.
Furthermore, given that the various particles which make up the
system are non-interacting, we expect their instantaneous positions to be completely
uncorrelated with one another. This immediately implies that
the multi-particle wavefunction
 can
be written as the product of
can
be written as the product of 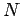 independent single-particle
wavefunctions: i.e.,
independent single-particle
wavefunctions: i.e.,
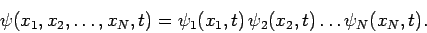 |
(430) |
Here,
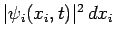 is the probability of finding the
is the probability of finding the
 th particle between
th particle between 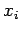 and
and 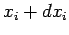 at time
at time  . This probability
is completely unaffected by the positions of the other particles. It
is evident that
. This probability
is completely unaffected by the positions of the other particles. It
is evident that 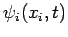 must satisfy the normalization constraint
must satisfy the normalization constraint
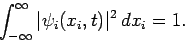 |
(431) |
If this is the case then the normalization constraint (418) for the
multi-particle wavefunction is automatically satisfied.
Equation (430) illustrates an important point in quantum mechanics: namely, that we can generally write the total wavefunction of a many degree of freedom system as a product of different wavefunctions corresponding to each degree
of freedom.
According to Eqs. (428) and (430), the time-dependent
Schrödinger equation (423) for a system of 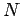 non-interacting
particles factorizes into
non-interacting
particles factorizes into 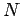 independent equations of the form
independent equations of the form
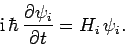 |
(432) |
Assuming that
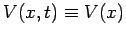 , the time-independent Schrödinger equation (425)
also factorizes to give
, the time-independent Schrödinger equation (425)
also factorizes to give
 |
(433) |
where
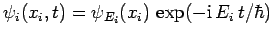 ,
and
,
and 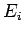 is the energy of the
is the energy of the  th particle.
Hence, a multi-particle state of definite energy
th particle.
Hence, a multi-particle state of definite energy 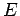 has a
wavefunction of the form
has a
wavefunction of the form
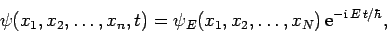 |
(434) |
where
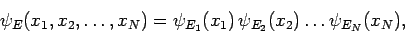 |
(435) |
and
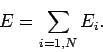 |
(436) |
Clearly, for the
case of non-interacting particles, the energy of
the whole system is simply the sum of the energies of the component
particles.



Next: Two-Particle Systems
Up: Multi-Particle Systems
Previous: Fundamental Concepts
Richard Fitzpatrick
2010-07-20
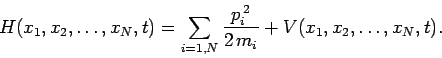
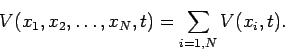
![]() non-interacting
particles factorizes into
non-interacting
particles factorizes into ![]() independent equations of the form
independent equations of the form