


Next: Non-Interacting Particles
Up: Multi-Particle Systems
Previous: Introduction
Fundamental Concepts
We have already seen that the instantaneous
state of a system consisting of a single non-relativistic particle, whose position coordinate
is 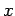 , is fully specified by
a complex wavefunction
, is fully specified by
a complex wavefunction 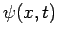 . This wavefunction is interpreted
as follows. The probability of finding the particle between
. This wavefunction is interpreted
as follows. The probability of finding the particle between 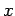 and
and
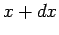 at time
at time  is given by
is given by
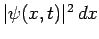 . This interpretation only makes sense if the wavefunction is
normalized such that
. This interpretation only makes sense if the wavefunction is
normalized such that
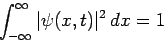 |
(417) |
at all times. The physical significance of this normalization requirement is
that the probability of the particle being found anywhere on the 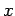 -axis
must always be unity (which corresponds to certainty).
-axis
must always be unity (which corresponds to certainty).
Consider a system containing 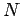 non-relativistic particles, labeled
non-relativistic particles, labeled  , moving in one dimension. Let
, moving in one dimension. Let 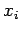 and
and 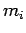 be the position coordinate
and mass, respectively, of the
be the position coordinate
and mass, respectively, of the  th particle.
By analogy with the single-particle case, the instantaneous state of a multi-particle system is
specified by a complex wavefunction
th particle.
By analogy with the single-particle case, the instantaneous state of a multi-particle system is
specified by a complex wavefunction
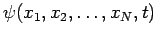 .
The probability of finding the first particle between
.
The probability of finding the first particle between 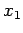 and
and 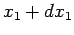 ,
the second particle between
,
the second particle between 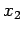 and
and 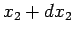 , etc., at time
, etc., at time
 is given by
is given by
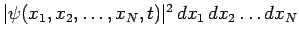 .
It follows that the wavefunction must satisfy the normalization condition
.
It follows that the wavefunction must satisfy the normalization condition
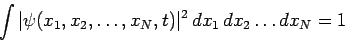 |
(418) |
at all times, where the integration is taken over all
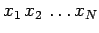 space.
space.
In a single-particle system, position is represented by the algebraic operator 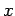 ,
whereas momentum is represented by the differential operator
,
whereas momentum is represented by the differential operator
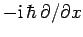 (see Sect. 4.6). By analogy,
in a multi-particle system, the position of the
(see Sect. 4.6). By analogy,
in a multi-particle system, the position of the  th particle
is represented by the algebraic operator
th particle
is represented by the algebraic operator 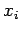 , whereas the corresponding
momentum is represented by the differential operator
, whereas the corresponding
momentum is represented by the differential operator
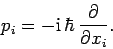 |
(419) |
Since the 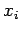 are independent variables (i.e.,
are independent variables (i.e.,
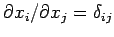 ), we conclude that the
various position and momentum operators satisfy the following commutation
relations:
), we conclude that the
various position and momentum operators satisfy the following commutation
relations:
Now, we know, from Sect. 4.10, that two dynamical variables
can only be (exactly) measured simultaneously if the operators which represent
them in quantum mechanics commute with one another. Thus,
it is clear, from the above commutation relations, that the only restriction
on measurement in a one-dimensional multi-particle system is that it is impossible to
simultaneously measure the position and momentum of the same
particle. Note, in particular, that a knowledge of the position or momentum of a given
particle does not in any way preclude a similar knowledge for a different
particle. The commutation relations (420)-(422) illustrate
an important point in quantum mechanics: namely, that operators corresponding to different degrees
of freedom of a dynamical system tend to commute with one another.
In this case, the different degrees of freedom correspond to the different
motions of the various particles making up the system.
Finally, if
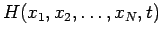 is the Hamiltonian of the system then
the multi-particle wavefunction
is the Hamiltonian of the system then
the multi-particle wavefunction
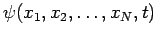 satisfies
the usual time-dependent Schrödinger equation [see Eq. (199)]
satisfies
the usual time-dependent Schrödinger equation [see Eq. (199)]
 |
(423) |
Likewise, a multi-particle state of definite energy 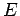 (i.e., an
eigenstate of the Hamiltonian with eigenvalue
(i.e., an
eigenstate of the Hamiltonian with eigenvalue 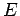 ) is written (see Sect. 4.12)
) is written (see Sect. 4.12)
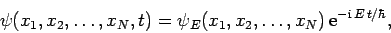 |
(424) |
where the stationary wavefunction  satisfies the time-independent
Schrödinger equation [see Eq. (296)]
satisfies the time-independent
Schrödinger equation [see Eq. (296)]
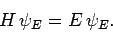 |
(425) |
Here,  is assumed not to be an explicit function of
is assumed not to be an explicit function of  .
.



Next: Non-Interacting Particles
Up: Multi-Particle Systems
Previous: Introduction
Richard Fitzpatrick
2010-07-20
![]() non-relativistic particles, labeled
non-relativistic particles, labeled ![]() , moving in one dimension. Let
, moving in one dimension. Let ![]() and
and ![]() be the position coordinate
and mass, respectively, of the
be the position coordinate
and mass, respectively, of the ![]() th particle.
By analogy with the single-particle case, the instantaneous state of a multi-particle system is
specified by a complex wavefunction
th particle.
By analogy with the single-particle case, the instantaneous state of a multi-particle system is
specified by a complex wavefunction
![]() .
The probability of finding the first particle between
.
The probability of finding the first particle between ![]() and
and ![]() ,
the second particle between
,
the second particle between ![]() and
and ![]() , etc., at time
, etc., at time
![]() is given by
is given by
![]() .
It follows that the wavefunction must satisfy the normalization condition
.
It follows that the wavefunction must satisfy the normalization condition
![]() ,
whereas momentum is represented by the differential operator
,
whereas momentum is represented by the differential operator
![]() (see Sect. 4.6). By analogy,
in a multi-particle system, the position of the
(see Sect. 4.6). By analogy,
in a multi-particle system, the position of the ![]() th particle
is represented by the algebraic operator
th particle
is represented by the algebraic operator ![]() , whereas the corresponding
momentum is represented by the differential operator
, whereas the corresponding
momentum is represented by the differential operator
![]() are independent variables (i.e.,
are independent variables (i.e.,
![]() ), we conclude that the
various position and momentum operators satisfy the following commutation
relations:
), we conclude that the
various position and momentum operators satisfy the following commutation
relations:
![]() is the Hamiltonian of the system then
the multi-particle wavefunction
is the Hamiltonian of the system then
the multi-particle wavefunction
![]() satisfies
the usual time-dependent Schrödinger equation [see Eq. (199)]
satisfies
the usual time-dependent Schrödinger equation [see Eq. (199)]