


Next: Exercises (N.B. Neglect spin
Up: Multi-Particle Systems
Previous: Two-Particle Systems
Identical Particles
Consider a system consisting of two identical particles of mass  .
As before, the instantaneous state of the system is specified by the
complex wavefunction
.
As before, the instantaneous state of the system is specified by the
complex wavefunction
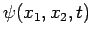 . However, the only thing
which this wavefunction tells us is that the probability of finding the
first particle between
. However, the only thing
which this wavefunction tells us is that the probability of finding the
first particle between 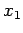 and
and 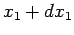 , and the second
between
, and the second
between 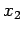 and
and 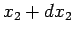 , at time
, at time  is
is
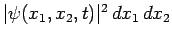 . However, since the particles are
identical, this must be the same as the probability of finding the
first particle between
. However, since the particles are
identical, this must be the same as the probability of finding the
first particle between 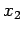 and
and 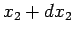 , and the second
between
, and the second
between 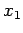 and
and 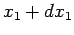 , at time
, at time  (since, in both
cases, the physical outcome of the measurement is exactly the same).
Hence, we conclude that
(since, in both
cases, the physical outcome of the measurement is exactly the same).
Hence, we conclude that
 |
(451) |
or
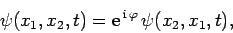 |
(452) |
where 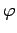 is a real constant. However, if we swap the labels on
particles 1 and 2 (which are, after all, arbitrary for identical particles), and repeat the argument, we also conclude that
is a real constant. However, if we swap the labels on
particles 1 and 2 (which are, after all, arbitrary for identical particles), and repeat the argument, we also conclude that
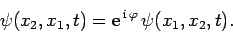 |
(453) |
Hence,
 |
(454) |
The only solutions to the above equation are 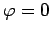 and
and 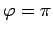 .
Thus, we infer that for a system consisting of two identical particles, the wavefunction
must be either symmetric or anti-symmetric under interchange
of particle labels: i.e., either
.
Thus, we infer that for a system consisting of two identical particles, the wavefunction
must be either symmetric or anti-symmetric under interchange
of particle labels: i.e., either
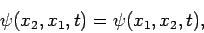 |
(455) |
or
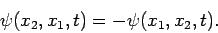 |
(456) |
The above argument can easily be extended to systems containing more
than two identical particles.
It turns out that whether the wavefunction of a
system containing many identical particles is symmetric or anti-symmetric
under interchange of the labels on any two particles is determined by the nature
of the particles themselves. Particles with wavefunctions which are symmetric under
label interchange
are said to obey Bose-Einstein statistics, and
are called bosons--for instance, photons are bosons. Particles with
wavefunctions which are anti-symmetric
under label interchange are said to obey Fermi-Dirac
statistics, and are called fermions--for instance, electrons,
protons, and neutrons are fermions.
Consider a system containing two identical and non-interacting bosons.
Let  be a properly normalized, single-particle, stationary wavefunction corresponding to a state of definite energy
be a properly normalized, single-particle, stationary wavefunction corresponding to a state of definite energy 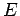 .
The stationary wavefunction of the
whole system is written
.
The stationary wavefunction of the
whole system is written
![\begin{displaymath}
\psi_{E boson}(x_1,x_2) = \frac{1}{\sqrt{2}}\left[\psi(x_1,E_a) \psi(x_2,E_b)+\psi(x_2,E_a) \psi(x_1,E_b)\right],
\end{displaymath}](img1145.png) |
(457) |
when the energies of the two particles are 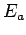 and
and 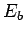 . This
expression automatically satisfies the symmetry requirement on the
wavefunction. Incidentally, since the particles are
identical, we cannot be sure which particle
has energy
. This
expression automatically satisfies the symmetry requirement on the
wavefunction. Incidentally, since the particles are
identical, we cannot be sure which particle
has energy 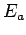 , and which has energy
, and which has energy 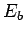 --only that one particle
has energy
--only that one particle
has energy 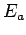 , and the other
, and the other 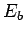 .
.
For a system consisting of two identical and non-interacting fermions,
the stationary wavefunction of the whole system takes
the form
![\begin{displaymath}
\psi_{E fermion}(x_1,x_2) = \frac{1}{\sqrt{2}}\left[\psi(x_1,E_a) \psi(x_2,E_b)-\psi(x_2,E_a) \psi(x_1,E_b)\right],
\end{displaymath}](img1148.png) |
(458) |
Again, this expression automatically satisfies the symmetry requirement on
the wavefunction. Note that if 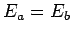 then the total wavefunction
becomes zero everywhere. Now, in quantum mechanics, a null wavefunction
corresponds to the absence of a state. We thus conclude that it
is impossible for the two fermions in our system to occupy the
same single-particle stationary state.
then the total wavefunction
becomes zero everywhere. Now, in quantum mechanics, a null wavefunction
corresponds to the absence of a state. We thus conclude that it
is impossible for the two fermions in our system to occupy the
same single-particle stationary state.
Finally, if the two particles are somehow distinguishable then the stationary
wavefunction of the system is simply
 |
(459) |
Let us evaluate the variance of the distance, 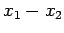 , between the
two particles, using the above three wavefunctions. It is easily
demonstrated that if the particles are distinguishable then
, between the
two particles, using the above three wavefunctions. It is easily
demonstrated that if the particles are distinguishable then
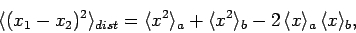 |
(460) |
where
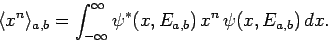 |
(461) |
For the case of two identical bosons, we find
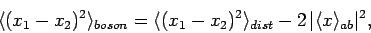 |
(462) |
where
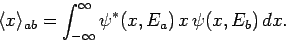 |
(463) |
Here, we have assumed that  , so that
, so that
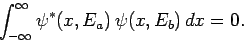 |
(464) |
Finally, for the case of two identical fermions, we obtain
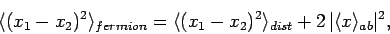 |
(465) |
Equation (462) shows that
the symmetry requirement on the total wavefunction of two identical bosons forces the
particles to be, on average, closer together than two similar distinguishable
particles. Conversely, Eq. (465) shows that the symmetry requirement on the total wavefunction of two identical fermions forces the
particles to be, on average, further apart than two similar distinguishable
particles. However, the strength of this effect depends on square of the magnitude of
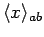 , which measures the overlap between the
wavefunctions
, which measures the overlap between the
wavefunctions 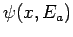 and
and 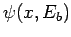 . It is evident, then, that
if these two wavefunctions do not overlap to any great extent then identical
bosons or fermions will act very much like distinguishable particles.
. It is evident, then, that
if these two wavefunctions do not overlap to any great extent then identical
bosons or fermions will act very much like distinguishable particles.
For a system containing 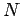 identical and non-interacting fermions,
the anti-symmetric stationary wavefunction of the system
is written
identical and non-interacting fermions,
the anti-symmetric stationary wavefunction of the system
is written
This expression is known as the Slater determinant, and automatically
satisfies the symmetry requirements on the wavefunction.
Here, the energies of the particles are
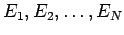 .
Note, again, that if any two particles in the system have the same energy
(i.e., if
.
Note, again, that if any two particles in the system have the same energy
(i.e., if 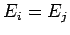 for some
for some 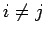 )
then the total wavefunction is null. We conclude that it is impossible
for any two identical fermions in a multi-particle system to
occupy the same single-particle stationary state. This important result is known as
the Pauli exclusion principle.
)
then the total wavefunction is null. We conclude that it is impossible
for any two identical fermions in a multi-particle system to
occupy the same single-particle stationary state. This important result is known as
the Pauli exclusion principle.
Subsections



Next: Exercises (N.B. Neglect spin
Up: Multi-Particle Systems
Previous: Two-Particle Systems
Richard Fitzpatrick
2010-07-20
![]() be a properly normalized, single-particle, stationary wavefunction corresponding to a state of definite energy
be a properly normalized, single-particle, stationary wavefunction corresponding to a state of definite energy ![]() .
The stationary wavefunction of the
whole system is written
.
The stationary wavefunction of the
whole system is written
![]() , between the
two particles, using the above three wavefunctions. It is easily
demonstrated that if the particles are distinguishable then
, between the
two particles, using the above three wavefunctions. It is easily
demonstrated that if the particles are distinguishable then
![]() identical and non-interacting fermions,
the anti-symmetric stationary wavefunction of the system
is written
identical and non-interacting fermions,
the anti-symmetric stationary wavefunction of the system
is written
![$\displaystyle \frac{1}{\sqrt{N!}} \left\vert
\begin{array}{cccc}
\psi(x_1,E_1)&...
...0.5ex]
\psi(x_1,E_N)&\psi(x_2,E_N)&\ldots&\psi(x_N,E_N)
\end{array}\right\vert.$](img1163.png)