


Next: Schrödinger's Equation
Up: Wave-Particle Duality
Previous: Evolution of Wave Packets
Heisenberg's Uncertainty Principle
According to the analysis contained in the previous two sections, a particle
wave packet which is initially localized in  -space with characteristic
width
-space with characteristic
width 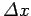 is also localized in
is also localized in 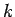 -space with characteristic
width
-space with characteristic
width
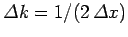 . However, as time progresses,
the width of the wave packet in
. However, as time progresses,
the width of the wave packet in  -space increases, whilst that of the wave packet in
-space increases, whilst that of the wave packet in 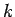 -space stays the same. [After all, our
previous analysis obtained
-space stays the same. [After all, our
previous analysis obtained 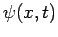 from Eq. (97), but assumed
that
from Eq. (97), but assumed
that 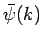 was given by Eq. (93) at all times.] Hence,
in general, we can say that
was given by Eq. (93) at all times.] Hence,
in general, we can say that
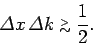 |
(118) |
Furthermore, we can think of 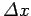 and
and
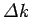 as
characterizing our uncertainty regarding the values of the particle's
position and wavenumber, respectively.
as
characterizing our uncertainty regarding the values of the particle's
position and wavenumber, respectively.
Now, a measurement of a particle's wavenumber, 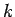 , is equivalent to
a measurement of its momentum,
, is equivalent to
a measurement of its momentum, 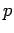 , since
, since 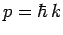 . Hence,
an uncertainty in
. Hence,
an uncertainty in 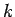 of order
of order
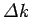 translates to
an uncertainty in
translates to
an uncertainty in 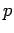 of order
of order
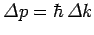 .
It follows from the above inequality that
.
It follows from the above inequality that
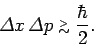 |
(119) |
This is the famous Heisenberg uncertainty principle,
first proposed by Werner Heisenberg in 1927.
According to this principle, it is impossible to simultaneously
measure the position and momentum of a particle (exactly). Indeed, a good knowledge
of the particle's position implies a poor knowledge of its momentum,
and vice versa. Note that the uncertainty principle is a direct consequence of representing particles as waves.
It can be seen from Eqs. (79), (105), and (112)
that at large 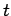 a particle wavefunction of original width
a particle wavefunction of original width
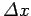 (at
(at 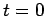 ) spreads out such that its spatial extent becomes
) spreads out such that its spatial extent becomes
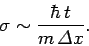 |
(120) |
It is easily demonstrated that this spreading is a consequence of the
uncertainty principle. Since the initial uncertainty in the particle's
position is 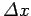 , it follows that the uncertainty in its
momentum is of order
, it follows that the uncertainty in its
momentum is of order
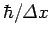 . This translates to an uncertainty
in velocity of
. This translates to an uncertainty
in velocity of
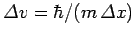 . Thus,
if we imagine that parts of the wavefunction propagate at
. Thus,
if we imagine that parts of the wavefunction propagate at
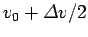 , and others at
, and others at
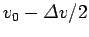 , where
, where 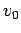 is
the mean propagation velocity, then the wavefunction will
spread as time progresses. Indeed, at large
is
the mean propagation velocity, then the wavefunction will
spread as time progresses. Indeed, at large 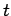 we expect the
width of the wavefunction to be
we expect the
width of the wavefunction to be
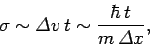 |
(121) |
which is identical to Eq. (120). Evidently, the spreading of
a particle wavefunction must be interpreted as an increase
in our uncertainty regarding the particle's position, rather than
an increase in the spatial extent of the particle itself.
Figure 8:
Heisenberg's microscope.
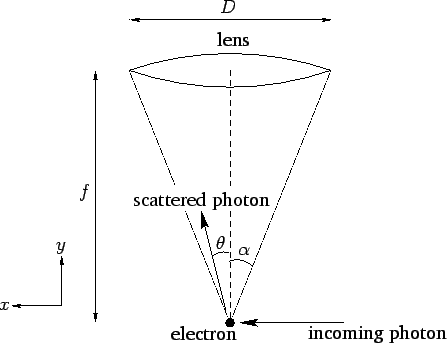 |
Figure 8 illustrates a famous thought experiment known as
Heisenberg's microscope. Suppose that we try to image an
electron using a simple optical system in which the objective lens is of
diameter 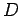 and focal-length
and focal-length 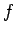 . (In practice, this would only
be possible using extremely short wavelength light.) It is a
well-known result in optics that such a system has a
minimum angular resolving power of
. (In practice, this would only
be possible using extremely short wavelength light.) It is a
well-known result in optics that such a system has a
minimum angular resolving power of 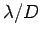 , where
, where 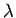 is the wavelength of the light illuminating the electron. If the electron is placed at the focus
of the lens, which is where the minimum resolving power is achieved, then this translates to a uncertainty in the
electron's transverse position of
is the wavelength of the light illuminating the electron. If the electron is placed at the focus
of the lens, which is where the minimum resolving power is achieved, then this translates to a uncertainty in the
electron's transverse position of
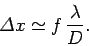 |
(122) |
However,
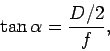 |
(123) |
where 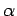 is the half-angle subtended by the lens at the electron.
Assuming that
is the half-angle subtended by the lens at the electron.
Assuming that 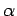 is small, we can write
is small, we can write
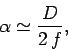 |
(124) |
so
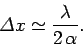 |
(125) |
It follows that we can reduce the uncertainty in the electron's position
by minimizing the ratio
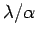 : i.e., by using short
wavelength radiation, and a wide-angle lens.
: i.e., by using short
wavelength radiation, and a wide-angle lens.
Let us now examine Heisenberg's microscope from a quantum mechanical
point of view. According to quantum mechanics, the electron is imaged
when it scatters an incoming photon towards the objective lens.
Let the wavevector of the incoming photon have the 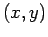 components
components 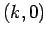 . See Fig. 8. If the scattered photon
subtends an angle
. See Fig. 8. If the scattered photon
subtends an angle 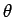 with the center-line of the optical
system, as shown in the figure, then its wavevector is written
with the center-line of the optical
system, as shown in the figure, then its wavevector is written
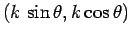 . Here,
we are ignoring any wavelength shift of the photon on scattering--i.e.,
the magnitude of the
. Here,
we are ignoring any wavelength shift of the photon on scattering--i.e.,
the magnitude of the 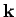 -vector is assumed to be the same before and after scattering.
Thus, the change in the
-vector is assumed to be the same before and after scattering.
Thus, the change in the  -component of the photon's wavevector
is
-component of the photon's wavevector
is
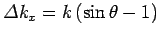 . This translates to a change
in the photon's
. This translates to a change
in the photon's  -component of momentum of
-component of momentum of
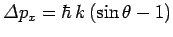 . By momentum conservation, the
electron's
. By momentum conservation, the
electron's  -momentum will change by an equal and opposite
amount. However,
-momentum will change by an equal and opposite
amount. However, 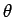 can range all the way from
can range all the way from 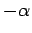 to
to
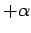 , and the scattered photon will still be collected by
the imaging system. It follows that the uncertainty in the electron's
momentum is
, and the scattered photon will still be collected by
the imaging system. It follows that the uncertainty in the electron's
momentum is
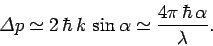 |
(126) |
Note that in order to reduce the uncertainty in the momentum we need to maximize
the ratio
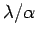 . This is exactly the opposite of what we
need to do to reduce the uncertainty in the position. Multiplying the
previous two equations, we obtain
. This is exactly the opposite of what we
need to do to reduce the uncertainty in the position. Multiplying the
previous two equations, we obtain
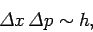 |
(127) |
which is essentially the uncertainty principle.
According to Heisenberg's microscope, the uncertainty principle follows
from two facts. First, it is impossible to measure any property of a microscopic dynamical system without
disturbing the system somewhat. Second, particle and light energy and momentum are quantized.
Hence, there is a limit to how small we can make the aforementioned
disturbance. Thus, there is an irreducible uncertainty in certain measurements which is a consequence of the act of measurement itself.



Next: Schrödinger's Equation
Up: Wave-Particle Duality
Previous: Evolution of Wave Packets
Richard Fitzpatrick
2010-07-20
![]() , is equivalent to
a measurement of its momentum,
, is equivalent to
a measurement of its momentum, ![]() , since
, since ![]() . Hence,
an uncertainty in
. Hence,
an uncertainty in ![]() of order
of order
![]() translates to
an uncertainty in
translates to
an uncertainty in ![]() of order
of order
![]() .
It follows from the above inequality that
.
It follows from the above inequality that
![]() a particle wavefunction of original width
a particle wavefunction of original width
![]() (at
(at ![]() ) spreads out such that its spatial extent becomes
) spreads out such that its spatial extent becomes
![]() and focal-length
and focal-length ![]() . (In practice, this would only
be possible using extremely short wavelength light.) It is a
well-known result in optics that such a system has a
minimum angular resolving power of
. (In practice, this would only
be possible using extremely short wavelength light.) It is a
well-known result in optics that such a system has a
minimum angular resolving power of ![]() , where
, where ![]() is the wavelength of the light illuminating the electron. If the electron is placed at the focus
of the lens, which is where the minimum resolving power is achieved, then this translates to a uncertainty in the
electron's transverse position of
is the wavelength of the light illuminating the electron. If the electron is placed at the focus
of the lens, which is where the minimum resolving power is achieved, then this translates to a uncertainty in the
electron's transverse position of
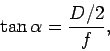
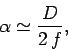
![]() components
components ![]() . See Fig. 8. If the scattered photon
subtends an angle
. See Fig. 8. If the scattered photon
subtends an angle ![]() with the center-line of the optical
system, as shown in the figure, then its wavevector is written
with the center-line of the optical
system, as shown in the figure, then its wavevector is written
![]() . Here,
we are ignoring any wavelength shift of the photon on scattering--i.e.,
the magnitude of the
. Here,
we are ignoring any wavelength shift of the photon on scattering--i.e.,
the magnitude of the ![]() -vector is assumed to be the same before and after scattering.
Thus, the change in the
-vector is assumed to be the same before and after scattering.
Thus, the change in the ![]() -component of the photon's wavevector
is
-component of the photon's wavevector
is
![]() . This translates to a change
in the photon's
. This translates to a change
in the photon's ![]() -component of momentum of
-component of momentum of
![]() . By momentum conservation, the
electron's
. By momentum conservation, the
electron's ![]() -momentum will change by an equal and opposite
amount. However,
-momentum will change by an equal and opposite
amount. However, ![]() can range all the way from
can range all the way from ![]() to
to
![]() , and the scattered photon will still be collected by
the imaging system. It follows that the uncertainty in the electron's
momentum is
, and the scattered photon will still be collected by
the imaging system. It follows that the uncertainty in the electron's
momentum is