


Next: Evolution of Wave Packets
Up: Wave-Particle Duality
Previous: Quantum Particles
Wave Packets
The above discussion suggests that the wavefunction of a massive particle
of momentum 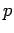 and energy
and energy 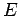 , moving in the positive
, moving in the positive  -direction, can be written
-direction, can be written
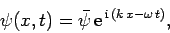 |
(82) |
where 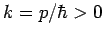 and
and
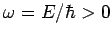 . Here,
. Here, 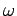 and
and
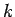 are linked via the dispersion relation (79). Expression (82) represents a plane wave whose maxima and
minima propagate in the positive
are linked via the dispersion relation (79). Expression (82) represents a plane wave whose maxima and
minima propagate in the positive  -direction
with the phase velocity
-direction
with the phase velocity 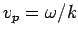 . As we have seen, this phase velocity is only half of the classical velocity of a massive particle.
. As we have seen, this phase velocity is only half of the classical velocity of a massive particle.
From before, the most reasonable physical interpretation of the wavefunction is that
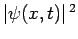 is proportional to the probability density of finding the particle
at position
is proportional to the probability density of finding the particle
at position  at time
at time 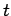 . However, the modulus squared of the wavefunction (82) is
. However, the modulus squared of the wavefunction (82) is
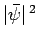 , which depends on neither
, which depends on neither  nor
nor 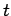 . In other words, this wavefunction represents a particle
which is equally likely to be found anywhere on the
. In other words, this wavefunction represents a particle
which is equally likely to be found anywhere on the  -axis at all times.
Hence, the fact that the maxima and minima of the wavefunction propagate at
a phase velocity which does not correspond to the classical particle velocity does not have any real physical consequences.
-axis at all times.
Hence, the fact that the maxima and minima of the wavefunction propagate at
a phase velocity which does not correspond to the classical particle velocity does not have any real physical consequences.
So, how can we write the wavefunction of a particle which is localized
in  : i.e., a particle which is more likely to be found at some
positions on the
: i.e., a particle which is more likely to be found at some
positions on the  -axis than at others? It turns out that we can achieve this goal by forming
a linear combination of plane waves of different wavenumbers:
i.e.,
-axis than at others? It turns out that we can achieve this goal by forming
a linear combination of plane waves of different wavenumbers:
i.e.,
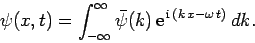 |
(83) |
Here, 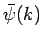 represents the complex amplitude of plane waves of wavenumber
represents the complex amplitude of plane waves of wavenumber 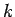 in this combination. In writing the above expression,
we are relying on the assumption that particle waves are superposable:
i.e., it is possible to add two valid wave solutions to form a third valid wave solution.
The ultimate justification for this assumption is that particle waves
satisfy a differential wave equation which is linear in
in this combination. In writing the above expression,
we are relying on the assumption that particle waves are superposable:
i.e., it is possible to add two valid wave solutions to form a third valid wave solution.
The ultimate justification for this assumption is that particle waves
satisfy a differential wave equation which is linear in 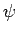 . As we
shall see, in Sect. 3.15, this is indeed the case. Incidentally, a plane wave which varies as
. As we
shall see, in Sect. 3.15, this is indeed the case. Incidentally, a plane wave which varies as
![$\exp[{\rm i} (k x-\omega t)]$](img321.png) and has a negative
and has a negative 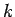 (but positive
(but positive 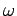 ) propagates
in the negative
) propagates
in the negative  -direction at the phase velocity
-direction at the phase velocity 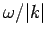 . Hence, the superposition (83)
includes both forward and backward propagating waves.
. Hence, the superposition (83)
includes both forward and backward propagating waves.
Now, there is a useful mathematical theorem, known as Fourier's theorem, which states that if
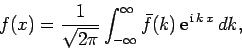 |
(84) |
then
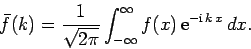 |
(85) |
Here, 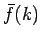 is known as the Fourier transform of the
function
is known as the Fourier transform of the
function 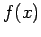 . We can use Fourier's theorem to find the
. We can use Fourier's theorem to find the 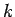 -space function
-space function 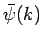 which generates any given
which generates any given  -space wavefunction
-space wavefunction 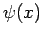 at a given time.
at a given time.
For instance, suppose that at 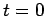 the wavefunction of our particle takes the
form
the wavefunction of our particle takes the
form
![\begin{displaymath}
\psi(x,0) \propto \exp\left[{\rm i} k_0 x - \frac{(x-x_0)^{ 2}}{4 ({\mit\Delta}x)^{ 2}}\right].
\end{displaymath}](img328.png) |
(86) |
Thus, the initial probability density of the particle is written
![\begin{displaymath}
\vert\psi(x,0)\vert^{ 2} \propto \exp\left[- \frac{(x-x_0)^{ 2}}{2 ({\mit\Delta}x)^{ 2}}\right].
\end{displaymath}](img329.png) |
(87) |
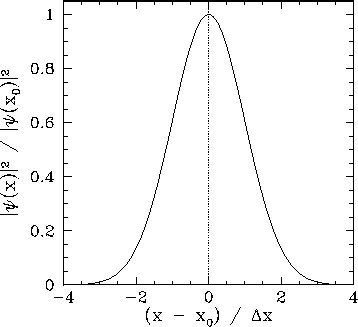
This particular probability distribution is called a Gaussian distribution, and is plotted in Fig. 7.
It can be seen that a measurement of the particle's position is most
likely to yield the value 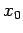 , and very
unlikely to yield a value which differs from
, and very
unlikely to yield a value which differs from 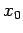 by more than
by more than
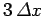 . Thus, (86) is the wavefunction of a particle
which is initially localized around
. Thus, (86) is the wavefunction of a particle
which is initially localized around 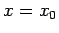 in some region whose width is
of order
in some region whose width is
of order
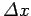 . This type of wavefunction is
known as a wave packet.
. This type of wavefunction is
known as a wave packet.
Figure 7:
A Gaussian probability distribution in  -space.
-space.
 |
Now, according to Eq. (83),
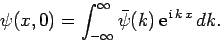 |
(88) |
Hence, we can employ Fourier's theorem to invert this expression to give
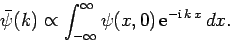 |
(89) |
Making use of Eq. (86),
we obtain
![\begin{displaymath}
\bar{\psi}(k) \propto
{\rm e}^{-{\rm i} (k-k_0) x_0}\int_{...
...0) (x-x_0) - \frac{(x-x_0)^2}{4 ({\mit\Delta}x)^2}\right]dx.
\end{displaymath}](img337.png) |
(90) |
Changing the variable of integration to
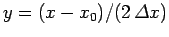 , this reduces to
, this reduces to
![\begin{displaymath}
\bar{\psi}(k) \propto {\rm e}^{-{\rm i} k x_0}
\int_{-\infty}^{\infty}\exp\left[-{\rm i} \beta y - y^2\right] dy,
\end{displaymath}](img339.png) |
(91) |
where
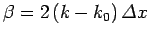 . The above equation
can be rearranged to give
. The above equation
can be rearranged to give
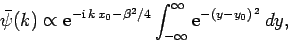 |
(92) |
where
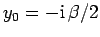 . The integral now just reduces to a number,
as can easily be seen by making the change of variable
. The integral now just reduces to a number,
as can easily be seen by making the change of variable 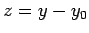 .
Hence, we obtain
.
Hence, we obtain
![\begin{displaymath}
\bar{\psi}(k) \propto \exp\left[-{\rm i} k x_0 - \frac{(k-k_0)^{ 2}}{4 ({\mit\Delta}k)^2}\right],
\end{displaymath}](img344.png) |
(93) |
where
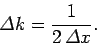 |
(94) |
Now, if
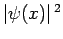 is proportional to the probability density of a measurement of the
particle's position yielding the value
is proportional to the probability density of a measurement of the
particle's position yielding the value  then it stands to reason that
then it stands to reason that
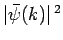 is proportional to the probability density of a measurement of the
particle's wavenumber yielding the value
is proportional to the probability density of a measurement of the
particle's wavenumber yielding the value 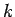 . (Recall that
. (Recall that 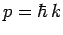 ,
so a measurement of the particle's wavenumber,
,
so a measurement of the particle's wavenumber, 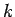 , is equivalent to a measurement of the particle's
momentum,
, is equivalent to a measurement of the particle's
momentum, 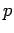 ). According to Eq. (93),
). According to Eq. (93),
![\begin{displaymath}
\vert\bar{\psi}(k)\vert^{ 2} \propto \exp\left[- \frac{(k-k_0)^{ 2}}{2 ({\mit\Delta}k)^{ 2}}\right].
\end{displaymath}](img349.png) |
(95) |
Note that this probability distribution is a Gaussian in 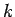 -space. See
Eq. (87) and Fig. 7. Hence, a measurement of
-space. See
Eq. (87) and Fig. 7. Hence, a measurement of 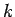 is
most likely to yield the value
is
most likely to yield the value 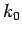 , and very unlikely to yield
a value which differs from
, and very unlikely to yield
a value which differs from 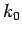 by more than
by more than
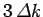 . Incidentally, a Gaussian is the only mathematical function
in
. Incidentally, a Gaussian is the only mathematical function
in  -space which has the same form as its Fourier transform in
-space which has the same form as its Fourier transform in 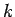 -space.
-space.
We have just seen that a Gaussian probability distribution of characteristic
width
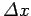 in
in  -space [see Eq. (87)] transforms to a Gaussian probability distribution of characteristic width
-space [see Eq. (87)] transforms to a Gaussian probability distribution of characteristic width
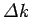 in
in 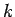 -space [see Eq. (95)],
where
-space [see Eq. (95)],
where
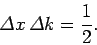 |
(96) |
This illustrates an important property of wave packets. Namely, if we wish to
construct a packet which is very localized in  -space (i.e., if
-space (i.e., if 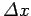 is small) then we need
to combine plane waves with a very wide range of different
is small) then we need
to combine plane waves with a very wide range of different 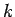 -values
(i.e.,
-values
(i.e., 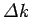 will be large). Conversely, if we only combine
plane waves whose wavenumbers differ by a small amount (i.e., if
will be large). Conversely, if we only combine
plane waves whose wavenumbers differ by a small amount (i.e., if
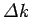 is small) then the resulting wave packet will be very
extended in
is small) then the resulting wave packet will be very
extended in  -space (i.e.,
-space (i.e., 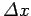 will be large).
will be large).



Next: Evolution of Wave Packets
Up: Wave-Particle Duality
Previous: Quantum Particles
Richard Fitzpatrick
2010-07-20
![]() is proportional to the probability density of finding the particle
at position
is proportional to the probability density of finding the particle
at position ![]() at time
at time ![]() . However, the modulus squared of the wavefunction (82) is
. However, the modulus squared of the wavefunction (82) is
![]() , which depends on neither
, which depends on neither ![]() nor
nor ![]() . In other words, this wavefunction represents a particle
which is equally likely to be found anywhere on the
. In other words, this wavefunction represents a particle
which is equally likely to be found anywhere on the ![]() -axis at all times.
Hence, the fact that the maxima and minima of the wavefunction propagate at
a phase velocity which does not correspond to the classical particle velocity does not have any real physical consequences.
-axis at all times.
Hence, the fact that the maxima and minima of the wavefunction propagate at
a phase velocity which does not correspond to the classical particle velocity does not have any real physical consequences.
![]() : i.e., a particle which is more likely to be found at some
positions on the
: i.e., a particle which is more likely to be found at some
positions on the ![]() -axis than at others? It turns out that we can achieve this goal by forming
a linear combination of plane waves of different wavenumbers:
i.e.,
-axis than at others? It turns out that we can achieve this goal by forming
a linear combination of plane waves of different wavenumbers:
i.e.,
![]() the wavefunction of our particle takes the
form
the wavefunction of our particle takes the
form
![\begin{displaymath}
\bar{\psi}(k) \propto
{\rm e}^{-{\rm i} (k-k_0) x_0}\int_{...
...0) (x-x_0) - \frac{(x-x_0)^2}{4 ({\mit\Delta}x)^2}\right]dx.
\end{displaymath}](img337.png)
![]() is proportional to the probability density of a measurement of the
particle's position yielding the value
is proportional to the probability density of a measurement of the
particle's position yielding the value ![]() then it stands to reason that
then it stands to reason that
![]() is proportional to the probability density of a measurement of the
particle's wavenumber yielding the value
is proportional to the probability density of a measurement of the
particle's wavenumber yielding the value ![]() . (Recall that
. (Recall that ![]() ,
so a measurement of the particle's wavenumber,
,
so a measurement of the particle's wavenumber, ![]() , is equivalent to a measurement of the particle's
momentum,
, is equivalent to a measurement of the particle's
momentum, ![]() ). According to Eq. (93),
). According to Eq. (93),
![]() in
in ![]() -space [see Eq. (87)] transforms to a Gaussian probability distribution of characteristic width
-space [see Eq. (87)] transforms to a Gaussian probability distribution of characteristic width
![]() in
in ![]() -space [see Eq. (95)],
where
-space [see Eq. (95)],
where