


Next: Wave Packets
Up: Wave-Particle Duality
Previous: Classical Particles
Just as light waves sometimes exhibit particle-like properties, it turns
out that massive particles sometimes exhibit wave-like properties.
For instance, it is possible to obtain a double-slit interference pattern
from a stream of mono-energetic electrons passing through two closely
spaced narrow slits. Now, the
effective wavelength of the electrons can be determined by measuring the width of the light and
dark bands in the interference pattern [see Eq. (68)]. It is found that
 |
(73) |
The same relation is found for other types of particles. The above
wavelength is called the de Broglie wavelength, after Louis de Broglie
who first suggested that particles should have wave-like properties in 1923.
Note that the de Broglie wavelength is generally pretty small. For instance,
that of an electron is
![\begin{displaymath}
\lambda_e = 1.2\times 10^{-9} [E({\rm eV})]^{-1/2} {\rm m},
\end{displaymath}](img301.png) |
(74) |
where the electron energy is conveniently measured in units of electron-volts (eV).
(An electron accelerated from rest through a potential difference of 1000V
acquires an energy of 1000eV, and so on.) The de Broglie wavelength
of a proton is
![\begin{displaymath}
\lambda_p = 2.9\times 10^{-11} [E({\rm eV})]^{-1/2} {\rm m}.
\end{displaymath}](img302.png) |
(75) |
Given the smallness of the de Broglie wavelengths of common particles,
it is actually quite difficult to do particle interference experiments.
In general, in order to perform an effective interference experiment, the spacing
of the slits must not be too much greater than the wavelength of the wave.
Hence, particle interference experiments require either very low energy particles (since
 ), or very closely spaced slits. Usually
the ``slits'' consist of crystals, which act a bit like diffraction gratings
with a characteristic spacing of order the inter-atomic spacing (which is
generally about
), or very closely spaced slits. Usually
the ``slits'' consist of crystals, which act a bit like diffraction gratings
with a characteristic spacing of order the inter-atomic spacing (which is
generally about 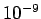 m).
m).
Equation (73) can be rearranged to give
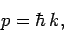 |
(76) |
which is exactly the same as the relation between momentum and
wavenumber that we obtained earlier for photons [see Eq. (62)].
For the case of a particle moving the three dimensions, the above
relation generalizes to give
 |
(77) |
where 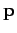 is the particle's vector momentum, and
is the particle's vector momentum, and 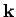 its wavevector.
It follows that the momentum of a quantum particle, and, hence, its velocity, is always parallel to its wavevector.
its wavevector.
It follows that the momentum of a quantum particle, and, hence, its velocity, is always parallel to its wavevector.
Since the relation (62) between momentum and wavenumber applies to both photons and massive particles,
it seems plausible that the closely related relation (60)
between energy and wave angular frequency should also apply to both photons
and particles. If this is the case, and we can write
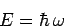 |
(78) |
for particle waves, then Eqs. (72) and (76) yield the
following dispersion relation for such waves:
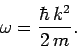 |
(79) |
Now, we saw earlier that a plane wave propagates at the
so-called phase velocity,
 |
(80) |
However, according to the above dispersion relation, a
particle plane wave propagates at
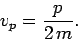 |
(81) |
Note, from Eq. (71), that this is only half of the classical particle
velocity. Does this imply that the dispersion relation (79) is
incorrect? Let us investigate further.



Next: Wave Packets
Up: Wave-Particle Duality
Previous: Classical Particles
Richard Fitzpatrick
2010-07-20

![]() ), or very closely spaced slits. Usually
the ``slits'' consist of crystals, which act a bit like diffraction gratings
with a characteristic spacing of order the inter-atomic spacing (which is
generally about
), or very closely spaced slits. Usually
the ``slits'' consist of crystals, which act a bit like diffraction gratings
with a characteristic spacing of order the inter-atomic spacing (which is
generally about ![]() m).
m).