


Next: Quantum Interference of Light
Up: Wave-Particle Duality
Previous: Quantum Theory of Light
Let us now consider the classical interference of light waves. Figure 5
shows a standard double-slit interference experiment in which monochromatic plane light waves are normally incident on two narrow parallel
slits which are a distance 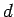 apart. The light from the two slits is projected onto
a screen a distance
apart. The light from the two slits is projected onto
a screen a distance 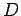 behind them, where
behind them, where 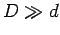 .
.
Figure 5:
Classical double-slit interference of light.
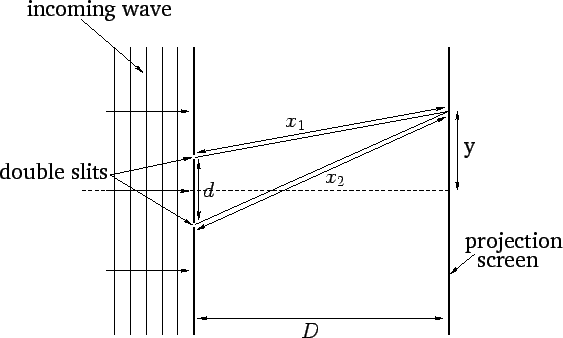 |
Consider some point
on the screen which is located a distance 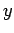 from the centre-line, as shown in the figure.
Light from the first slit travels a distance
from the centre-line, as shown in the figure.
Light from the first slit travels a distance 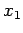 to get to this point, whereas
light from the second slit travels a slightly different distance
to get to this point, whereas
light from the second slit travels a slightly different distance 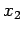 . It is
easily demonstrated that
. It is
easily demonstrated that
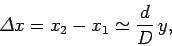 |
(63) |
provided 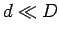 .
It follows from Eq. (46), and the well-known fact that light waves are superposible, that the wavefunction at the point in
question can be written
.
It follows from Eq. (46), and the well-known fact that light waves are superposible, that the wavefunction at the point in
question can be written
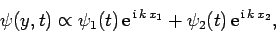 |
(64) |
where 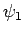 and
and 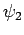 are the wavefunctions at the first and
second slits, respectively.
However,
are the wavefunctions at the first and
second slits, respectively.
However,
 |
(65) |
since the two slits are assumed to be
illuminated by in-phase light waves of equal amplitude. (Note that we are ignoring the difference in amplitude
of the waves from the two slits at the screen, due to the slight difference between 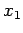 and
and 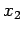 , compared to the difference in their phases.
This is reasonable provided
, compared to the difference in their phases.
This is reasonable provided 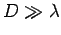 .) Now, the intensity (i.e., the energy flux) of the
light at some point on the projection screen is approximately equal to the energy density of the light at this point times the velocity of light (provided that
.) Now, the intensity (i.e., the energy flux) of the
light at some point on the projection screen is approximately equal to the energy density of the light at this point times the velocity of light (provided that 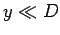 ). Hence, it follows from Eq. (56)
that the light intensity on the screen a distance
). Hence, it follows from Eq. (56)
that the light intensity on the screen a distance 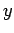 from the center-line is
from the center-line is
 |
(66) |
Using Eqs. (63)-(66), we obtain
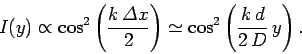 |
(67) |
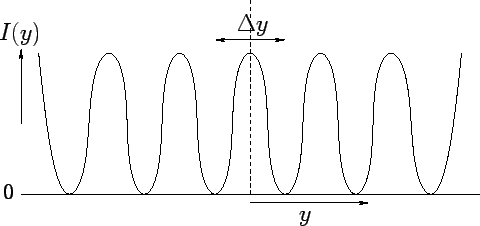
Figure 6 shows the characteristic interference pattern corresponding to the above expression. This pattern consists of equally spaced light and dark bands
of characteristic width
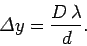 |
(68) |
Figure 6:
Classical double-slit interference pattern.
 |



Next: Quantum Interference of Light
Up: Wave-Particle Duality
Previous: Quantum Theory of Light
Richard Fitzpatrick
2010-07-20

![]() from the centre-line, as shown in the figure.
Light from the first slit travels a distance
from the centre-line, as shown in the figure.
Light from the first slit travels a distance ![]() to get to this point, whereas
light from the second slit travels a slightly different distance
to get to this point, whereas
light from the second slit travels a slightly different distance ![]() . It is
easily demonstrated that
. It is
easily demonstrated that