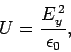Next: Photoelectric Effect
Up: Wave-Particle Duality
Previous: Representation of Waves via
Classical Light Waves
Consider a classical, monochromatic, linearly polarized, plane light wave,
propagating through a vacuum in the 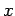 -direction. It is convenient to characterize a light wave
(which is, of course, a type of electromagnetic wave) by specifying its associated
electric field. Suppose that the wave is polarized such that this
electric field oscillates in the
-direction. It is convenient to characterize a light wave
(which is, of course, a type of electromagnetic wave) by specifying its associated
electric field. Suppose that the wave is polarized such that this
electric field oscillates in the 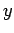 -direction. (According to standard
electromagnetic theory, the magnetic field oscillates in the
-direction. (According to standard
electromagnetic theory, the magnetic field oscillates in the 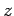 -direction, in phase with the electric field, with an amplitude which is that of the electric field divided by the
velocity of light in vacuum.) Now, the
electric field can be conveniently represented in terms of a complex wavefunction:
-direction, in phase with the electric field, with an amplitude which is that of the electric field divided by the
velocity of light in vacuum.) Now, the
electric field can be conveniently represented in terms of a complex wavefunction:
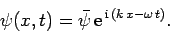 |
(46) |
Here,
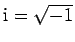 ,
, 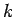 and
and 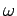 are real parameters, and
are real parameters, and 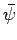 is a complex wave amplitude. By convention, the
physical electric field is the real part of the above expression.
Suppose that
is a complex wave amplitude. By convention, the
physical electric field is the real part of the above expression.
Suppose that
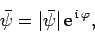 |
(47) |
where 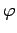 is real. It follows that the physical electric field
takes the form
is real. It follows that the physical electric field
takes the form
![\begin{displaymath}
E_y(x,t) = {\rm Re}[\psi(x,t)] = \vert\bar{\psi}\vert \cos(k x-\omega t +\varphi),
\end{displaymath}](img231.png) |
(48) |
where 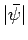 is the amplitude of the electric oscillation,
is the amplitude of the electric oscillation, 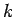 the wavenumber,
the wavenumber, 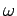 the
angular frequency, and
the
angular frequency, and 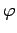 the phase angle. In addition,
the phase angle. In addition,
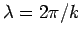 is the wavelength, and
is the wavelength, and
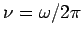 the frequency (in hertz).
the frequency (in hertz).
According to standard electromagnetic theory, the frequency and wavelength of light waves are related according to
the well-known expression
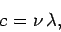 |
(49) |
or, equivalently,
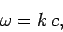 |
(50) |
where
 .
Equations (48) and (50) yield
.
Equations (48) and (50) yield
![\begin{displaymath}
E_y(x,t) =\vert\bar{\psi}\vert \cos\left(k [x-(\omega/k) ...
...)= \vert\bar{\psi}\vert \cos\left(k [x-c t]+\varphi\right).
\end{displaymath}](img237.png) |
(51) |
Note that 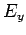 depends on
depends on 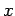 and
and  only via the
combination
only via the
combination 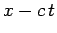 . It follows that the wave maxima and minima satisfy
. It follows that the wave maxima and minima satisfy
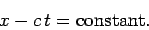 |
(52) |
Thus, the wave maxima and minima propagate in the 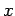 -direction at the fixed velocity
-direction at the fixed velocity
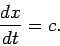 |
(53) |
An expression, such as (50), which determines the wave angular frequency
as a function of the wavenumber, is generally termed a dispersion
relation. As we have already seen, and as is apparent from Eq. (51), the maxima and minima of a plane wave
propagate at the characteristic velocity
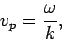 |
(54) |
which is known as the phase velocity. Hence, the dispersion relation (50) is effectively saying that the phase velocity of a plane light wave propagating through a vacuum always takes the fixed value  , irrespective
of its wavelength or frequency.
, irrespective
of its wavelength or frequency.
Now, from standard electromagnetic theory, the energy density (i.e., the energy per unit volume) of a
light wave is
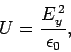 |
(55) |
where
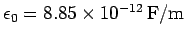 is the permittivity
of free space. Hence, it follows from Eqs. (46) and (48) that
is the permittivity
of free space. Hence, it follows from Eqs. (46) and (48) that
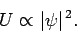 |
(56) |
Furthermore, a light wave possesses linear momentum, as well
as energy. This momentum is directed along the wave's direction of propagation, and is of density
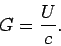 |
(57) |



Next: Photoelectric Effect
Up: Wave-Particle Duality
Previous: Representation of Waves via
Richard Fitzpatrick
2010-07-20